X 5 X 4 X 3
penangjazz
Nov 08, 2025 · 11 min read
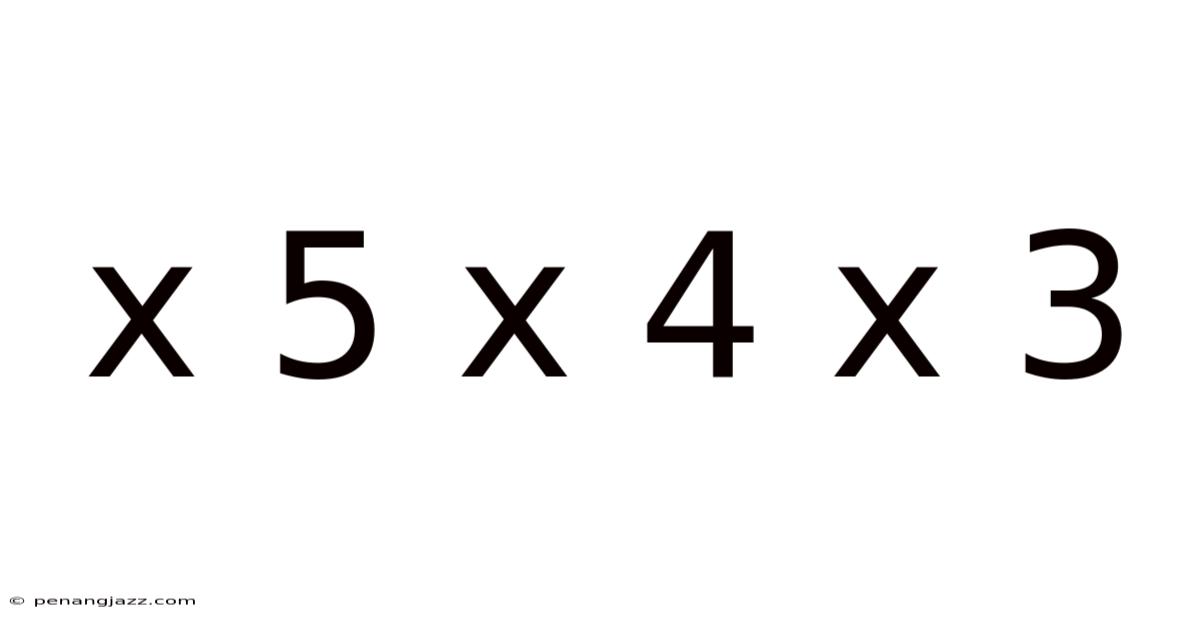
Table of Contents
Unraveling the Magic: Understanding and Mastering the 5x5x4x3 Puzzle
The world of combinatorial puzzles is vast and captivating, filled with challenges that test our spatial reasoning, problem-solving skills, and patience. Among these intriguing puzzles, the 5x5x4x3 stands out as a fascinating variation of the classic Rubik's Cube, offering a unique blend of complexity and beauty. This article delves into the intricacies of this rectangular prism puzzle, exploring its structure, notation, solving methods, and the underlying mathematical principles that govern its behavior. Whether you are a seasoned cuber or a curious beginner, this comprehensive guide will equip you with the knowledge and skills to conquer the 5x5x4x3 and appreciate its elegance.
Introduction to the 5x5x4x3
The 5x5x4x3, often referred to as a "shape mod" or "deformed cube," is a mechanical puzzle that modifies the traditional Rubik's Cube by altering its dimensions. Unlike a standard cube, which has equal dimensions on all three axes, the 5x5x4x3 has different lengths, widths, and heights, making it a rectangular prism. Specifically, it features 5 layers on one axis, 5 layers on another, 4 layers on a third, and 3 layers on the last axis.
This seemingly small change in shape introduces significant challenges in solving. The non-uniform dimensions lead to:
- Shape Shifting: The puzzle can deform significantly, making it difficult to recognize patterns and apply standard cube-solving algorithms.
- Parity Errors: The altered dimensions can lead to parity errors that are not present in a standard cube, requiring specialized algorithms to resolve.
- Visual Confusion: Identifying pieces and their correct positions becomes more difficult due to the distorted shape.
Despite these challenges, the 5x5x4x3 offers a rewarding solving experience. Its unique characteristics force cubers to adapt their strategies and develop a deeper understanding of cube mechanics. It's a puzzle that requires not only algorithmic knowledge but also a strong sense of spatial reasoning and a willingness to experiment.
Understanding the Anatomy of the 5x5x4x3
To effectively solve the 5x5x4x3, it's crucial to understand its component pieces and how they interact. The puzzle consists of three main types of pieces:
- Center Pieces: These pieces reside in the center of each face. On a standard 5x5, the center pieces are fixed relative to each other, defining the color scheme. However, on the 5x5x4x3, some center pieces can move relative to each other, requiring careful consideration during the solving process.
- Edge Pieces: Edge pieces are located between two faces. The 5x5x4x3 has different types of edge pieces depending on which faces they connect. Some edges span the 5x5 faces, others span the 5x4 faces, and still others span the 5x3 and 4x3 faces.
- Corner Pieces: Corner pieces reside at the corners of the puzzle, connecting three faces. The 5x5x4x3 has corner pieces that connect different combinations of the 5x5, 5x4, 5x3 and 4x3 faces.
Understanding the types and locations of these pieces is vital for developing a solving strategy. You'll need to identify which pieces can move freely and which are constrained, as well as how different moves affect their positions.
Notation for the 5x5x4x3
Clear notation is essential for communicating algorithms and solving strategies for any twisty puzzle. While standard Rubik's Cube notation can be adapted for the 5x5x4x3, some modifications and additions are necessary to account for the puzzle's unique structure.
Here's a breakdown of a possible notation system:
- Standard Face Turns: The basic notation for clockwise turns of the faces remains the same:
- F: Front face
- B: Back face
- R: Right face
- L: Left face
- U: Up face
- D: Down face
- Inverted Turns: An apostrophe (') indicates a counter-clockwise turn:
- F', B', R', L', U', D'
- Double Turns: A "2" indicates a 180-degree turn:
- F2, B2, R2, L2, U2, D2
- Slice Turns: To denote turns of the inner layers, we can use the following:
- M: Middle layer (parallel to L/R)
- E: Equator layer (parallel to U/D)
- S: Standing layer (parallel to F/B)
- Multiple Layer Turns: To denote turns of multiple layers, we can use a number before the face letter. For instance, 2R means turn the two rightmost layers together.
- Width-Specific Turns: Since the 5x5x4x3 has different dimensions, it's helpful to denote turns relative to the puzzle's orientation. For example, if the 5x5 faces are considered the front and back, and the 4x3 faces are on the top and bottom, we could use notations like:
- U4: Turn the top 4 layers of the puzzle.
- D3: Turn the bottom 3 layers of the puzzle.
- R5: Turn the right 5 layers of the puzzle.
- L5: Turn the left 5 layers of the puzzle.
This notation system provides a flexible way to describe various moves on the 5x5x4x3, allowing for clear communication of algorithms and solving techniques. It's essential to choose a notation system and stick to it consistently to avoid confusion.
A Layer-by-Layer Solving Method for the 5x5x4x3
A common and effective approach for solving the 5x5x4x3 is the layer-by-layer method, similar to how you might solve a standard Rubik's Cube. However, due to the shape-shifting nature of the puzzle, some steps require adaptation.
Here's a general outline of the layer-by-layer method:
- Solve the First Layer (e.g., the 3x4 face):
- Cross: Build a cross on one of the smaller faces. This involves finding the correct edge pieces and orienting them properly.
- Corners: Insert the corner pieces to complete the first layer.
- Solve the Second Layer (adjacent to the 3x4 face):
- This step involves inserting the edge pieces that belong to the second layer. Be mindful of the correct orientation and placement of each piece.
- Solve the Third Layer (adjacent to the previously solved layers):
- Insert the appropriate edges into this layer, paying attention to the correct orientations.
- Solve the Fourth Layer (e.g., the 5x3 face):
- Orient the Last Layer Edges: Use algorithms to orient the edges of the last layer so that the colors on the top face are correct, regardless of their position.
- Permute the Last Layer Edges: Use algorithms to cycle the edges of the last layer into their correct positions.
- Solve the Fifth Layer (e.g., the 5x5 face opposite the first layer):
- Orient the Last Layer Corners: Orient the corner pieces of the last layer so that the colors on the top face are correct, regardless of their position.
- Permute the Last Layer Corners: Use algorithms to cycle the corner pieces of the last layer into their correct positions.
- Solve the Sixth Layer (e.g., the 5x4 face opposite the previously solved layers):
- This step often involves recognizing and correcting parity errors.
- Correct Parity Errors:
- Due to the puzzle's shape, parity errors can occur, which are situations where the puzzle appears to be solved except for a few pieces that are swapped or oriented incorrectly. These errors require specific algorithms to fix. Common parity errors include:
- Edge Parity: Two edge pieces are swapped.
- Corner Parity: Two corner pieces are swapped.
- Center Parity: Two center pieces are swapped.
- Due to the puzzle's shape, parity errors can occur, which are situations where the puzzle appears to be solved except for a few pieces that are swapped or oriented incorrectly. These errors require specific algorithms to fix. Common parity errors include:
- Final Adjustments:
- Once all the layers are solved and parity errors are corrected, make any final adjustments to align the center pieces and ensure the puzzle is completely solved.
This layer-by-layer method provides a structured approach to solving the 5x5x4x3. Each step focuses on solving a specific part of the puzzle, making the overall process more manageable.
Advanced Techniques and Considerations
While the layer-by-layer method provides a solid foundation, mastering the 5x5x4x3 often involves learning advanced techniques and considering certain factors.
- Block Building: Instead of focusing solely on layers, consider building blocks of pieces that belong together. This can streamline the solving process and reduce the number of moves required.
- Intuitive F2L (First Two Layers): Adapt the F2L techniques from standard cube solving to solve the first two layers more efficiently. This involves pairing up corner and edge pieces and inserting them simultaneously.
- Recognizing and Predicting Shape Changes: Develop the ability to anticipate how different moves will affect the puzzle's shape. This will help you avoid getting stuck in situations where the puzzle becomes too deformed to solve easily.
- Understanding Center Piece Movement: Pay close attention to how the center pieces move relative to each other. In some cases, you may need to solve the centers before proceeding with other steps.
- Developing Custom Algorithms: As you become more familiar with the puzzle, consider developing your own algorithms to solve specific cases more efficiently.
- Practice and Patience: Solving the 5x5x4x3 takes practice and patience. Don't get discouraged if you encounter difficulties. Keep practicing, and you'll gradually improve your skills.
Mathematical Principles Underlying the 5x5x4x3
Like other twisty puzzles, the 5x5x4x3 is governed by mathematical principles from group theory and combinatorics. Understanding these principles can provide deeper insights into the puzzle's behavior and help you develop more effective solving strategies.
- Group Theory: The set of all possible moves on the 5x5x4x3, along with the operation of composition (performing one move after another), forms a mathematical group. This group has a finite number of elements, representing all the possible configurations of the puzzle. Group theory provides tools for analyzing the structure of this group and understanding the relationships between different moves.
- Combinatorics: Combinatorics deals with counting the number of possible arrangements of objects. In the case of the 5x5x4x3, combinatorics can be used to calculate the total number of possible states of the puzzle. This number is extremely large, highlighting the complexity of the puzzle.
- Parity: The concept of parity plays a crucial role in understanding parity errors. Parity refers to whether a permutation (rearrangement) is even or odd. In the context of the 5x5x4x3, parity errors occur when the puzzle is in a state that requires an odd permutation to solve, but the standard moves only allow for even permutations. This is why specific algorithms are needed to correct these errors.
While a deep understanding of group theory and combinatorics is not strictly necessary to solve the 5x5x4x3, it can provide a valuable framework for understanding the puzzle's underlying structure and developing more sophisticated solving techniques.
Resources for Learning and Improving
Numerous resources are available to help you learn and improve your 5x5x4x3 solving skills:
- Online Tutorials: Many websites and YouTube channels offer detailed tutorials on solving the 5x5x4x3. These tutorials often include step-by-step instructions, algorithms, and helpful tips.
- Online Forums and Communities: Online forums and communities dedicated to twisty puzzles are great places to ask questions, share your progress, and learn from other cubers.
- Cube Simulators: Cube simulators allow you to practice solving the 5x5x4x3 virtually. This can be a convenient way to experiment with different algorithms and strategies without having to physically manipulate the puzzle.
- Books and Guides: Several books and guides provide comprehensive information on twisty puzzles, including the 5x5x4x3.
- Practice, Practice, Practice: The best way to improve your 5x5x4x3 solving skills is to practice regularly. Set aside time each day or week to solve the puzzle, and gradually increase the difficulty of your challenges.
The Allure of Complex Puzzles
The 5x5x4x3 is more than just a puzzle; it's a testament to human ingenuity and our innate desire to solve complex problems. Its unique shape, challenging mechanics, and vast number of possible states make it a captivating and rewarding puzzle to master. By understanding its structure, notation, and solving methods, and by appreciating the underlying mathematical principles, you can unlock the secrets of the 5x5x4x3 and experience the satisfaction of conquering this intriguing puzzle. The world of twisty puzzles offers endless opportunities for exploration and intellectual stimulation. Embrace the challenge, and enjoy the journey of discovery!
Conclusion: Embracing the Challenge of the 5x5x4x3
The 5x5x4x3 puzzle presents a unique and captivating challenge for cubers of all skill levels. Its distorted shape and complex mechanics require a blend of algorithmic knowledge, spatial reasoning, and problem-solving skills. By understanding the puzzle's anatomy, mastering the notation, and employing effective solving methods, you can unravel the secrets of the 5x5x4x3 and experience the satisfaction of bringing order to chaos. Whether you are a seasoned cuber looking for a new challenge or a curious beginner eager to explore the world of twisty puzzles, the 5x5x4x3 offers a rewarding and intellectually stimulating experience. So, pick up a 5x5x4x3, embrace the challenge, and embark on a journey of discovery that will test your limits and expand your understanding of the fascinating world of combinatorial puzzles. Remember to be patient, persistent, and most importantly, to have fun! The solution awaits!
Latest Posts
Latest Posts
-
What Are The Forces Of Evolution
Nov 08, 2025
-
Is Hcl A Base Or Acid
Nov 08, 2025
-
Difference Between Real Gas And Ideal Gas
Nov 08, 2025
-
How To Find Domain Of A Logarithmic Function
Nov 08, 2025
-
Value Of Gas Constant R In Atm
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about X 5 X 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.