X 2 3 In Radical Form
penangjazz
Nov 27, 2025 · 8 min read
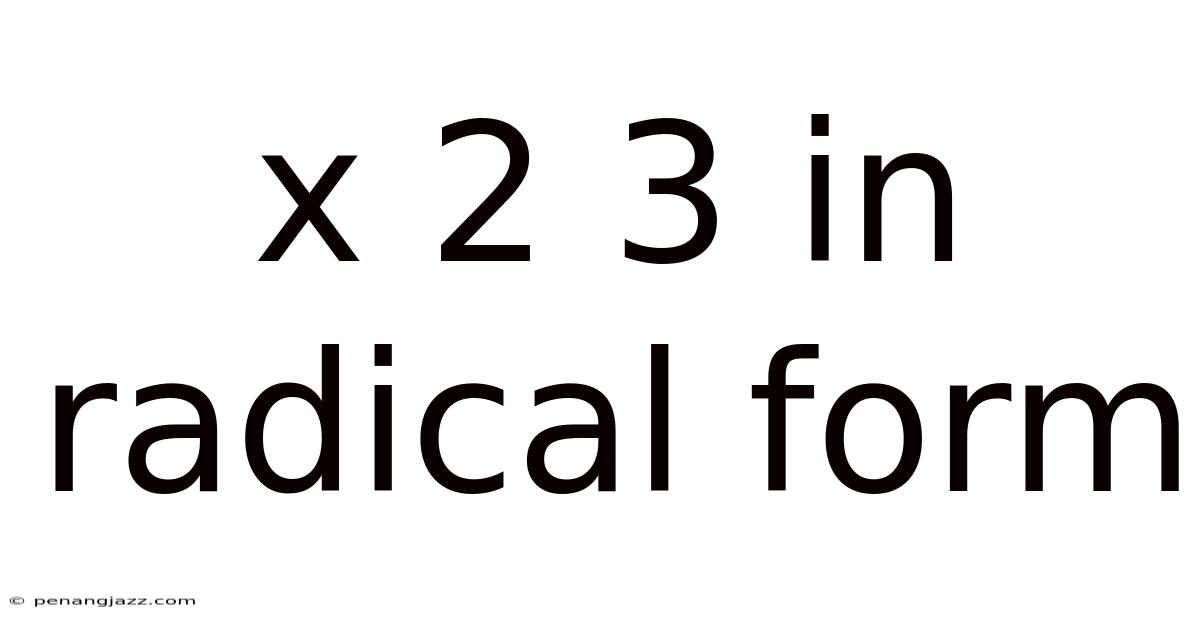
Table of Contents
Alright, let's dive into understanding how to express x^(2/3) in radical form. This involves understanding fractional exponents and their relationship to radicals (roots). We'll cover the basics of exponents and radicals, then move on to the specifics of converting fractional exponents, and finally apply this knowledge to x^(2/3) and other examples. This article will help you grasp the concept thoroughly and confidently handle such conversions.
Understanding Exponents and Radicals
Before we tackle fractional exponents, it's important to have a solid understanding of what exponents and radicals are in general.
-
Exponents: An exponent indicates how many times a base number is multiplied by itself. For example, in the expression a^n, a is the base and n is the exponent. This means you multiply a by itself n times.
- For instance, 2^3 = 2 * 2 * 2 = 8.
- Similarly, x^4 = x * x * x * x.
-
Radicals: A radical, often denoted by the symbol √, represents the root of a number. The most common type is the square root, which asks, "What number, when multiplied by itself, equals the number under the radical?"
- For example, √9 = 3, because 3 * 3 = 9.
- The number under the radical symbol is called the radicand.
Radicals can also have an index, which indicates what root to take. The square root has an implied index of 2. For other roots, the index is explicitly written.
- For example, ³√8 (cube root of 8) = 2, because 2 * 2 * 2 = 8. Here, the index is 3.
- Similarly, ⁴√16 (fourth root of 16) = 2, because 2 * 2 * 2 * 2 = 16. The index is 4.
Fractional Exponents: Bridging Exponents and Radicals
Fractional exponents are exponents that are expressed as fractions. They provide a powerful link between exponents and radicals. A fractional exponent can be understood in terms of both a power and a root.
The general form of a fractional exponent is a^(m/n), where:
- a is the base.
- m is the numerator, representing the power to which the base is raised.
- n is the denominator, representing the index of the root to be taken.
Therefore, a^(m/n) can be interpreted as:
- Taking the nth root of a, and then raising the result to the mth power: (ⁿ√a) ^ m.
- Raising a to the mth power, and then taking the nth root of the result: ⁿ√(a^m).
These two interpretations are equivalent. In mathematical notation:
a^(m/n) = (ⁿ√a)^m = ⁿ√(a^m)
Understanding the Components
To solidify your understanding, let's break down what each part of the fractional exponent signifies:
-
The Numerator (m): The numerator of the fraction acts as a regular exponent. It tells you what power to raise the base to. So, in a^(m/n), a is raised to the power of m.
-
The Denominator (n): The denominator of the fraction indicates the type of root you need to take. It's the index of the radical. So, in a^(m/n), you are taking the nth root of a.
Examples of Fractional Exponents
Let's look at some simple examples to illustrate the concept:
-
4^(1/2): Here, the base is 4, the numerator is 1, and the denominator is 2. This means we need to find the square root of 4 and then raise it to the power of 1.
- √4 = 2
- 2^1 = 2
- Therefore, 4^(1/2) = 2.
-
8^(1/3): In this case, the base is 8, the numerator is 1, and the denominator is 3. This means we need to find the cube root of 8 and then raise it to the power of 1.
- ³√8 = 2
- 2^1 = 2
- Therefore, 8^(1/3) = 2.
-
9^(3/2): Here, the base is 9, the numerator is 3, and the denominator is 2. This means we need to find the square root of 9 and then raise it to the power of 3.
- √9 = 3
- 3^3 = 27
- Therefore, 9^(3/2) = 27.
Alternatively, we can raise 9 to the power of 3 first, then take the square root:
- 9^3 = 729
- √729 = 27
- Therefore, 9^(3/2) = 27.
Converting x^(2/3) to Radical Form
Now, let's apply this understanding to our original problem: converting x^(2/3) to radical form.
Following the rule a^(m/n) = ⁿ√(a^m), we can directly translate x^(2/3) into radical form.
- The base is x.
- The numerator (power) is 2.
- The denominator (root index) is 3.
Therefore, x^(2/3) can be written as:
- ³√(x^2)
This is the radical form of x^(2/3). It means "the cube root of x squared."
Step-by-Step Breakdown
Here’s a detailed breakdown of the conversion:
-
Identify the base, numerator, and denominator:
- Base: x
- Numerator (m): 2
- Denominator (n): 3
-
Apply the formula a^(m/n) = ⁿ√(a^m):
- Substitute x for a, 2 for m, and 3 for n:
- x^(2/3) = ³√(x^2)
-
Write out the radical form:
- The cube root of x squared: ³√(x^2)
Further Examples and Practice
To reinforce your understanding, let’s work through some more examples of converting fractional exponents to radical form and vice versa.
Example 1: Converting to Radical Form
Convert y^(3/4) to radical form.
-
Identify components:
- Base: y
- Numerator: 3
- Denominator: 4
-
Apply the formula:
- y^(3/4) = ⁴√(y^3)
-
Result:
- The fourth root of y cubed: ⁴√(y^3)
Example 2: Converting to Radical Form
Convert (a + b)^(1/2) to radical form.
-
Identify components:
- Base: (a + b)
- Numerator: 1
- Denominator: 2
-
Apply the formula:
- (a + b)^(1/2) = √((a + b)^1) = √(a + b)
-
Result:
- The square root of (a + b): √(a + b)
Example 3: Converting from Radical Form to Fractional Exponent
Convert ⁵√(z^2) to fractional exponent form.
-
Identify components:
- Radicand: z^2
- Root index: 5
-
Apply the reverse formula:
- ⁵√(z^2) = z^(2/5)
-
Result:
- z to the power of 2/5: z^(2/5)
Example 4: Converting from Radical Form to Fractional Exponent
Convert ³√(1/x) to fractional exponent form.
-
Rewrite the radicand:
- ³√(1/x) = ³√(x^(-1))
-
Identify components:
- Radicand: x^(-1)
- Root index: 3
-
Apply the reverse formula:
- ³√(x^(-1)) = x^(-1/3)
-
Result:
- x to the power of -1/3: x^(-1/3)
Common Mistakes and How to Avoid Them
When working with fractional exponents and radicals, it’s easy to make mistakes. Here are some common pitfalls and how to avoid them:
-
Incorrectly Identifying the Numerator and Denominator: Make sure you correctly identify which number is the numerator (power) and which is the denominator (root index). Double-check your work to avoid swapping them.
-
Forgetting the Root Index: When converting from fractional exponent to radical form, don't forget to include the root index in the radical symbol. The denominator of the fractional exponent becomes the index of the radical.
-
Misinterpreting the Order of Operations: Remember that a^(m/n) means either (ⁿ√a)^m or ⁿ√(a^m). Both are equivalent, but make sure you perform the operations correctly. Evaluate the root or the power first, and then perform the remaining operation.
-
Ignoring Negative Exponents: If you encounter a negative exponent, remember that a^(-n) = 1/a^n. Handle the negative exponent first before converting to radical form. For example:
- x^(-1/2) = 1/x^(1/2) = 1/√x
-
Overcomplicating Simplification: Sometimes, you can simplify radicals or exponents before or after converting between forms. Look for opportunities to simplify the expression to make it easier to work with. For instance:
- (8x^3)^(2/3) = ³√((8x^3)^2) = ³√(64x^6) = 4x^2
Practical Applications
Understanding fractional exponents and radicals is not just an abstract mathematical exercise. These concepts are used in various fields:
-
Physics: In physics, radicals and exponents are used to describe relationships in mechanics, optics, and electromagnetism. For example, the period of a pendulum involves a square root, and the intensity of light decreases with the square of the distance.
-
Engineering: Engineers use radicals and exponents in structural analysis, signal processing, and control systems. For example, calculating stress and strain in materials often involves radicals.
-
Computer Graphics: In computer graphics, radicals and exponents are used for scaling, transformations, and lighting calculations. For example, shading models often use exponents to simulate realistic lighting effects.
-
Finance: Financial models often use exponents and roots for calculating compound interest, depreciation, and growth rates.
Conclusion
Converting x^(2/3) to radical form involves understanding the relationship between fractional exponents and radicals. The key takeaway is that the numerator of the fractional exponent is the power, and the denominator is the root index. Thus, x^(2/3) is expressed in radical form as ³√(x^2). By understanding these basic principles and practicing with examples, you can confidently convert any fractional exponent into its equivalent radical form and apply these concepts in various practical contexts. Mastering this conversion enhances your mathematical toolkit and allows you to tackle more complex problems in mathematics, science, and engineering. Remember to identify the base, numerator, and denominator accurately, and always double-check your work to avoid common mistakes.
Latest Posts
Latest Posts
-
Solution To A System Of Inequalities
Nov 27, 2025
-
Reacts With Acid Physical Or Chemical
Nov 27, 2025
-
What Is The Charge Of Br
Nov 27, 2025
-
Individuals Considered Members Of The Same Social Category Or Group
Nov 27, 2025
-
Punnett Square For Tay Sachs Disease
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about X 2 3 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.