Which Is Larger 3/16 Or 1/4
penangjazz
Nov 28, 2025 · 8 min read
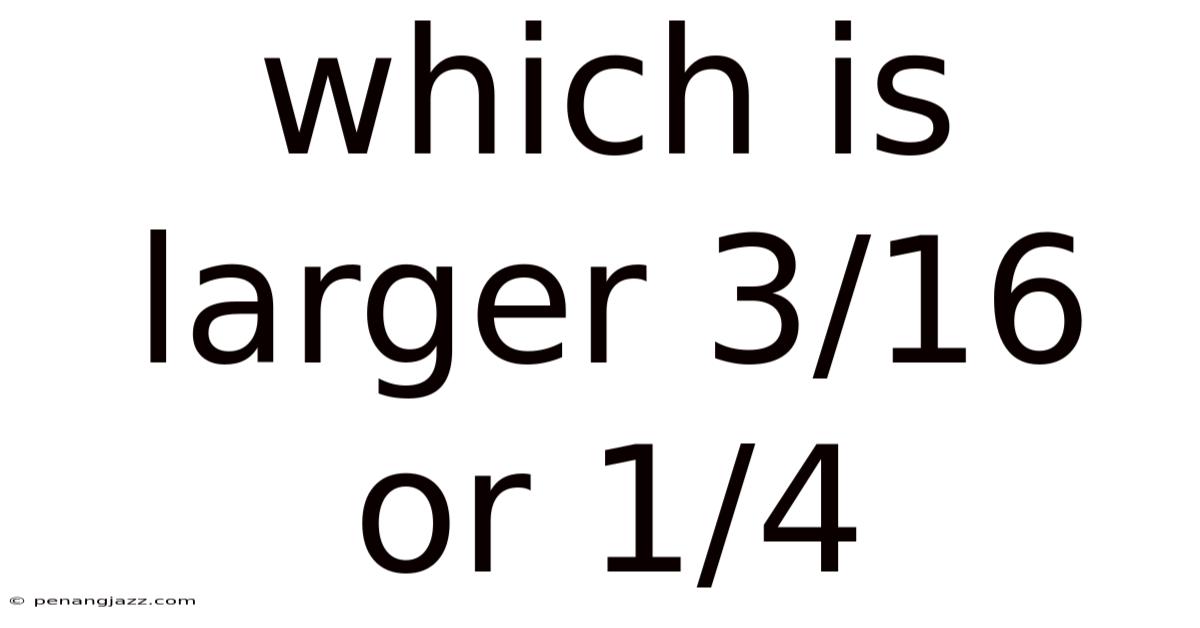
Table of Contents
To determine which fraction is larger, 3/16 or 1/4, we need to compare them effectively. Understanding fractions and different comparison methods is key to confidently determining their relative sizes. This article delves into a detailed exploration of these fractions, providing multiple approaches to ascertain which one holds a greater value, ensuring clarity and comprehension for readers of all backgrounds.
Understanding Fractions: The Basics
A fraction represents a part of a whole. It consists of two numbers: the numerator (the number on top) and the denominator (the number on the bottom). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
- Numerator: The number of parts we have.
- Denominator: The total number of equal parts.
For instance, in the fraction 3/16, the numerator is 3, and the denominator is 16. This means we have 3 parts out of a total of 16 equal parts. Similarly, in the fraction 1/4, the numerator is 1, and the denominator is 4, indicating that we have 1 part out of a total of 4 equal parts.
Method 1: Finding a Common Denominator
One of the most reliable methods to compare fractions is by finding a common denominator. This involves converting the fractions into equivalent fractions with the same denominator. Once the denominators are the same, we can easily compare the numerators to determine which fraction is larger.
Steps to Find a Common Denominator:
- Identify the Denominators:
- In our case, the denominators are 16 and 4.
- Find the Least Common Multiple (LCM):
- The LCM of 16 and 4 is the smallest number that both 16 and 4 divide into evenly.
- Multiples of 4: 4, 8, 12, 16, 20,...
- Multiples of 16: 16, 32, 48,...
- The LCM of 4 and 16 is 16.
- Convert the Fractions:
- We need to convert both fractions to have a denominator of 16.
- 3/16 already has the desired denominator, so it remains as 3/16.
- To convert 1/4 to a fraction with a denominator of 16, we multiply both the numerator and the denominator by the same number. Since 4 * 4 = 16, we multiply both the numerator and denominator of 1/4 by 4:
- (1 * 4) / (4 * 4) = 4/16
- Compare the Numerators:
- Now we compare the fractions 3/16 and 4/16.
- Since 4 is greater than 3, 4/16 is larger than 3/16.
Conclusion:
Since 4/16 is larger than 3/16, and 4/16 is equivalent to 1/4, we conclude that 1/4 is larger than 3/16.
Method 2: Cross-Multiplication
Cross-multiplication is a quick and efficient way to compare two fractions. It involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results.
Steps for Cross-Multiplication:
- Write down the fractions:
- 3/16 and 1/4
- Cross-multiply:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (4):
- 3 * 4 = 12
- Multiply the numerator of the second fraction (1) by the denominator of the first fraction (16):
- 1 * 16 = 16
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (4):
- Compare the Results:
- Compare the two products: 12 and 16.
- Since 16 is greater than 12, the second fraction (1/4) is larger than the first fraction (3/16).
Conclusion:
Cross-multiplication shows that 16 > 12, therefore 1/4 is larger than 3/16.
Method 3: Converting to Decimals
Another effective method to compare fractions is by converting them into decimal form. This allows for a straightforward comparison using decimal values.
Steps to Convert to Decimals:
- Divide the Numerator by the Denominator:
- For 3/16, divide 3 by 16:
- 3 ÷ 16 = 0.1875
- For 1/4, divide 1 by 4:
- 1 ÷ 4 = 0.25
- For 3/16, divide 3 by 16:
- Compare the Decimal Values:
- Compare 0.1875 and 0.25.
- Since 0.25 is greater than 0.1875, 1/4 is larger than 3/16.
Conclusion:
Converting to decimals, we find that 0.25 > 0.1875, thus 1/4 is larger than 3/16.
Method 4: Visual Representation
Sometimes, visualizing fractions can provide an intuitive understanding of their relative sizes. We can use diagrams or visual aids to represent the fractions and compare them.
Visual Comparison:
- Draw Two Identical Rectangles:
- These rectangles will represent the whole.
- Divide the First Rectangle into 16 Equal Parts:
- Shade 3 of these parts to represent 3/16.
- Divide the Second Rectangle into 4 Equal Parts:
- Shade 1 of these parts to represent 1/4.
- Compare the Shaded Areas:
- By visually comparing the shaded areas, it becomes clear that the area representing 1/4 is larger than the area representing 3/16.
Conclusion:
The visual representation clearly shows that 1/4 is larger than 3/16.
Method 5: Benchmarking
Benchmarking involves comparing the fractions to a common benchmark, such as 1/2 or 1/3. This can help in quickly determining the relative sizes of the fractions without performing complex calculations.
Benchmarking Steps:
- Choose a Benchmark:
- In this case, let's use 1/4 as a benchmark since we have one of the fractions as 1/4.
- Compare the Fractions to the Benchmark:
- We know that 1/4 is equal to 1/4.
- Now, we need to determine if 3/16 is less than, equal to, or greater than 1/4. We already know from previous methods that 3/16 is less than 1/4.
- Analyze the Comparison:
- Since 3/16 is less than 1/4, and 1/4 is equal to 1/4, it is clear that 1/4 is the larger fraction.
Conclusion:
Using benchmarking, we confirm that 1/4 is larger than 3/16.
Practical Applications of Fraction Comparison
Understanding how to compare fractions is crucial in various real-life situations. Here are a few examples:
- Cooking:
- When following a recipe, you might need to adjust ingredient quantities. Knowing whether 1/3 cup is more or less than 2/5 cup can ensure the recipe turns out correctly.
- Construction:
- In construction, measurements often involve fractions. For instance, a builder needs to know if a 3/8 inch gap is larger or smaller than a 1/4 inch gap to choose the right materials.
- Finance:
- When comparing investment returns, understanding fractions is essential. If one investment yields 1/5 return and another yields 2/9, knowing which fraction is larger helps in making informed financial decisions.
- Education:
- Students frequently encounter fractions in math and science problems. Being able to quickly and accurately compare fractions is vital for problem-solving.
- Daily Life:
- Dividing resources or time often involves fractions. For example, determining whether spending 1/3 of your day on work is more or less than 2/7 on leisure helps in time management.
Common Mistakes to Avoid
When comparing fractions, several common mistakes can lead to incorrect conclusions. Being aware of these pitfalls can help ensure accuracy.
- Assuming Larger Denominator Means Larger Fraction:
- It's a common misconception that a fraction with a larger denominator is always smaller. This is not true unless the numerators are the same. For example, 1/100 is smaller than 1/2, even though 100 is much larger than 2.
- Ignoring the Numerator:
- Focusing solely on the denominator without considering the numerator can lead to errors. The numerator indicates how many parts of the whole we have, so it's crucial for comparison.
- Incorrectly Finding the Common Denominator:
- Failing to find the correct least common multiple (LCM) can result in incorrect equivalent fractions, leading to a wrong comparison.
- Miscalculating Decimal Conversions:
- Errors in dividing the numerator by the denominator can lead to incorrect decimal values, affecting the comparison.
- Not Simplifying Fractions First:
- Sometimes, simplifying fractions before comparing them can make the process easier. Failing to simplify can complicate the comparison and increase the chance of errors.
- Rushing the Process:
- Rushing through the comparison without carefully checking each step can lead to mistakes. Taking the time to double-check calculations and comparisons can prevent errors.
Advanced Tips for Fraction Comparison
For those looking to deepen their understanding of fraction comparison, here are some advanced tips:
- Using Percentage Conversion:
- Convert fractions to percentages for easy comparison. Multiply the fraction by 100 to get its percentage value.
- 3/16 * 100 = 18.75%
- 1/4 * 100 = 25%
- Comparing 18.75% and 25% clearly shows that 1/4 is larger.
- Convert fractions to percentages for easy comparison. Multiply the fraction by 100 to get its percentage value.
- Estimating Fractions:
- Develop a sense of fraction magnitudes by estimating their values. For instance, recognizing that 3/16 is a little less than 1/5 and 1/4 is a common benchmark can help in quick estimations.
- Fraction Number Lines:
- Use number lines to visualize fractions and their relative positions. This can be particularly helpful for complex fractions.
- Comparing to 1/2:
- Quickly determine if a fraction is greater or less than 1/2. This can serve as a preliminary step in comparing multiple fractions.
- Understanding Fraction Properties:
- Grasp the properties of fractions, such as how increasing the numerator increases the fraction's value and increasing the denominator decreases the fraction's value (when the numerator is constant).
Conclusion
In summary, comparing fractions is a fundamental skill with wide-ranging applications. Whether using common denominators, cross-multiplication, decimal conversion, visual representation, or benchmarking, each method provides a clear pathway to determine the relative sizes of fractions. Through detailed explanations and practical examples, this article has demonstrated that 1/4 is larger than 3/16. By understanding these methods and avoiding common mistakes, anyone can confidently compare fractions in various contexts, from cooking to finance and beyond. The ability to accurately compare fractions not only enhances mathematical proficiency but also empowers informed decision-making in everyday life.
Latest Posts
Latest Posts
-
Law Of Independent Assortment Dna Crossing Over
Nov 28, 2025
-
In Photosynthesis What Are The Two Major Reactions
Nov 28, 2025
-
Why Melting Of Ice Is A Physical Change
Nov 28, 2025
-
What Coefficients Would Balance The Following Equation
Nov 28, 2025
-
Ar Kr And Xe Reactive Or Not Reactive
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 3/16 Or 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.