Which Graph Represents The Compound Inequality 3 N 1
penangjazz
Nov 22, 2025 · 9 min read
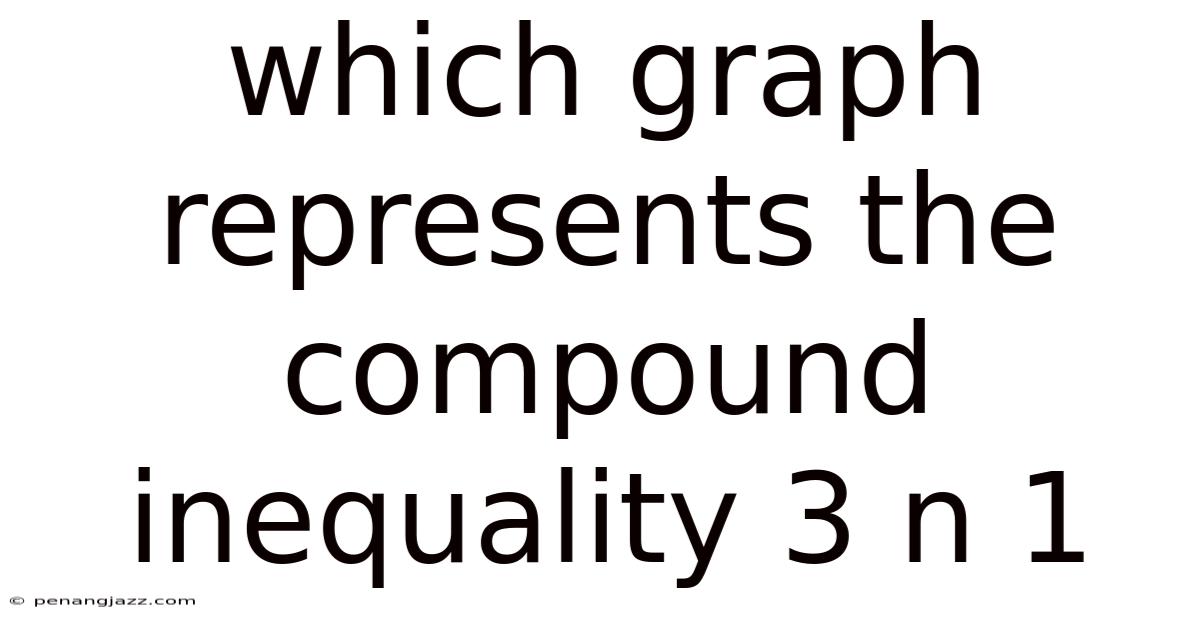
Table of Contents
Graphing compound inequalities can seem daunting at first, but breaking down the process into manageable steps makes it quite straightforward. Understanding the core principles of inequalities and how they translate visually on a number line is the key. In this article, we will focus on the compound inequality 3 ≥ n > 1, dissecting it to understand its components and ultimately illustrating how to represent it on a graph.
Understanding Compound Inequalities
Compound inequalities are essentially two or more inequalities combined into a single statement. They typically involve two inequalities connected by either "and" or "or." In the case of "and," both conditions must be true simultaneously. For "or," at least one of the conditions must be true. Our example, 3 ≥ n > 1, uses an implied "and," meaning 'n' must be less than or equal to 3 AND greater than 1.
Decoding 3 ≥ n > 1
Let's break down the compound inequality 3 ≥ n > 1:
- 3 ≥ n can be read as "3 is greater than or equal to n" or "n is less than or equal to 3."
- n > 1 can be read as "n is greater than 1."
Combining these, we're looking for all values of 'n' that are both greater than 1 and less than or equal to 3.
The Number Line: Visualizing Numbers
The number line is a simple yet powerful tool for visualizing numbers and their relationships. It's a straight line with numbers placed at equal intervals, extending infinitely in both positive and negative directions. Zero sits at the center, with positive numbers to the right and negative numbers to the left.
Graphing the Compound Inequality: Step-by-Step
Here's how to graph the compound inequality 3 ≥ n > 1 on a number line:
-
Draw the Number Line: Start by drawing a straight line. Mark zero in the middle and then add equally spaced intervals representing positive and negative numbers. You don't need to include every number; just enough to cover the range of values relevant to your inequality (in this case, around -1 to 5 should suffice).
-
Identify Key Values: The key values from our inequality are 1 and 3. Locate these points on your number line.
-
Representing "n > 1": Since 'n' is greater than 1 (but not equal to), we use an open circle (also sometimes referred to as a parenthesis) at 1. An open circle indicates that 1 is not included in the solution set.
-
Representing "3 ≥ n": Since 'n' is less than or equal to 3, we use a closed circle (also sometimes referred to as a bracket) at 3. A closed circle indicates that 3 is included in the solution set.
-
Shading the Solution Set: Because we want the values of 'n' that are both greater than 1 and less than or equal to 3, we shade the region of the number line between 1 and 3. This shaded area represents all the numbers that satisfy the compound inequality.
-
Final Representation: The finished graph should have an open circle at 1, a closed circle at 3, and the region between them shaded. This visually represents the solution set for 3 ≥ n > 1.
Examples and Further Clarification
Let's solidify our understanding with a few more examples and explore different ways to interpret the graph.
Example 1: Graphing n < -2 or n ≥ 1
This is an "or" compound inequality. We need to graph both inequalities and then combine the solutions.
- n < -2: Draw an open circle at -2 and shade the number line to the left (towards negative infinity).
- n ≥ 1: Draw a closed circle at 1 and shade the number line to the right (towards positive infinity).
The final graph will have two shaded regions: one to the left of -2 (excluding -2) and one to the right of 1 (including 1).
Example 2: Graphing -1 ≤ n ≤ 4
This is an "and" compound inequality.
- -1 ≤ n: Draw a closed circle at -1 and shade the number line to the right.
- n ≤ 4: Draw a closed circle at 4 and shade the number line to the left.
The final graph will have a shaded region between -1 and 4, including both -1 and 4 (because of the "equal to" part of the inequality).
Interpreting the Graph
The graph provides a visual representation of the solutions to the inequality. Any point on the shaded region of the number line represents a value that satisfies the inequality. For example, in our original inequality 3 ≥ n > 1, the number 2.5 is within the shaded region, meaning 2.5 is a solution. The number 0 is not in the shaded region and therefore is not a solution. Similarly, 1 is not a solution (due to the open circle), but 3 is a solution (due to the closed circle).
Interval Notation: An Alternative Representation
While graphs are excellent for visualizing inequalities, interval notation provides a concise algebraic way to represent the same information. Interval notation uses parentheses and brackets to indicate whether endpoints are included or excluded from the solution set.
- (a, b): Represents all numbers between a and b, excluding a and b.
- [a, b]: Represents all numbers between a and b, including a and b.
- (a, b]: Represents all numbers between a and b, excluding a but including b.
- [a, b): Represents all numbers between a and b, including a but excluding b.
- (-∞, a): Represents all numbers less than a (excluding a).
- (-∞, a]: Represents all numbers less than or equal to a.
- (a, ∞): Represents all numbers greater than a (excluding a).
- [a, ∞): Represents all numbers greater than or equal to a.
Applying Interval Notation to 3 ≥ n > 1
For the compound inequality 3 ≥ n > 1, the interval notation is (1, 3]. This reads as "all numbers greater than 1 (but not including 1) and less than or equal to 3 (including 3)." This directly corresponds to our graphical representation with the open circle at 1 and the closed circle at 3.
Interval Notation for "Or" Inequalities
For "or" inequalities, we use the union symbol (∪) to combine the separate intervals. For example, for the inequality n < -2 or n ≥ 1, the interval notation would be (-∞, -2) ∪ [1, ∞).
Common Mistakes and How to Avoid Them
Graphing inequalities is generally straightforward, but there are a few common mistakes to watch out for:
-
Incorrect Circle Type: The most common mistake is using the wrong type of circle (open or closed) at the key values. Remember, use an open circle for ">" or "<" (excluding the value) and a closed circle for "≥" or "≤" (including the value).
-
Shading in the Wrong Direction: Double-check which direction to shade. If 'n' is greater than a number, shade to the right. If 'n' is less than a number, shade to the left.
-
Misinterpreting Compound Inequalities: Make sure you understand the "and" and "or" conditions. "And" means both inequalities must be true, so you only shade the overlapping region. "Or" means at least one inequality must be true, so you shade all regions covered by either inequality.
-
Forgetting the Number Line: Always start by drawing a number line. This helps you visualize the numbers and the direction of the inequality.
-
Not Checking Your Work: After graphing, pick a number from the shaded region and plug it back into the original inequality. If the inequality holds true, you've likely graphed it correctly. If not, re-examine your graph.
Practical Applications of Inequalities
Inequalities aren't just abstract mathematical concepts; they have practical applications in various fields:
-
Computer Science: Inequalities are used in algorithms to define conditions for loops and conditional statements. For example, an algorithm might continue running as long as a certain variable remains less than a specific value.
-
Economics: Inequalities are used to model constraints and limitations. For example, a company might have a production capacity constraint, meaning it can only produce a certain number of units per day.
-
Engineering: Inequalities are used to define tolerances and safety margins. For example, an engineer might design a bridge to withstand loads exceeding a certain threshold.
-
Statistics: Inequalities are used in hypothesis testing and confidence intervals. For example, a researcher might determine that a drug is effective if the probability of a certain outcome is greater than a predefined significance level.
-
Everyday Life: Inequalities are used in everyday decision-making. For example, you might decide to take a certain route to work if the estimated travel time is less than 30 minutes. Or, you might choose a product based on whether its price is within your budget.
Understanding inequalities and how to represent them graphically can help you better understand and solve problems in these and other fields.
Advanced Concepts: Absolute Value Inequalities
Once you're comfortable with basic inequalities, you can move on to more advanced concepts like absolute value inequalities. The absolute value of a number is its distance from zero, regardless of direction. Therefore, solving absolute value inequalities often involves considering two separate cases.
Example: |x| < 3
This inequality means that the distance of 'x' from zero is less than 3. This translates into two inequalities:
- x < 3
- -x < 3, which is equivalent to x > -3
Combining these, we get -3 < x < 3. The graph would have open circles at -3 and 3, with the region between them shaded.
Example: |x| ≥ 2
This inequality means that the distance of 'x' from zero is greater than or equal to 2. This translates into two inequalities:
- x ≥ 2
- -x ≥ 2, which is equivalent to x ≤ -2
The graph would have a closed circle at -2, with the region to the left shaded, and a closed circle at 2, with the region to the right shaded.
Conclusion
Graphing inequalities, including compound inequalities like 3 ≥ n > 1, is a fundamental skill in algebra. It provides a visual representation of the solution set and helps to understand the relationships between numbers. By following the steps outlined in this article, practicing with examples, and being mindful of common mistakes, you can master the art of graphing inequalities and confidently apply this knowledge in various mathematical and real-world contexts. Remember to always double-check your work, use the correct circle type, and understand the implications of "and" and "or" conditions. With practice and attention to detail, you can become proficient in graphing inequalities and confidently tackle more advanced mathematical concepts.
Latest Posts
Latest Posts
-
What Is A Rhythm In Art
Nov 22, 2025
-
List Of Weak Acids And Weak Bases
Nov 22, 2025
-
Weak Base Strong Acid Titration Equivalence Point
Nov 22, 2025
-
Is The Ability To Make An Object Appear Larger
Nov 22, 2025
-
How To Find Total Resistance Of A Parallel Circuit
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Represents The Compound Inequality 3 N 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.