What Is The Lowest Common Multiple Of 3 And 4
penangjazz
Nov 21, 2025 · 9 min read
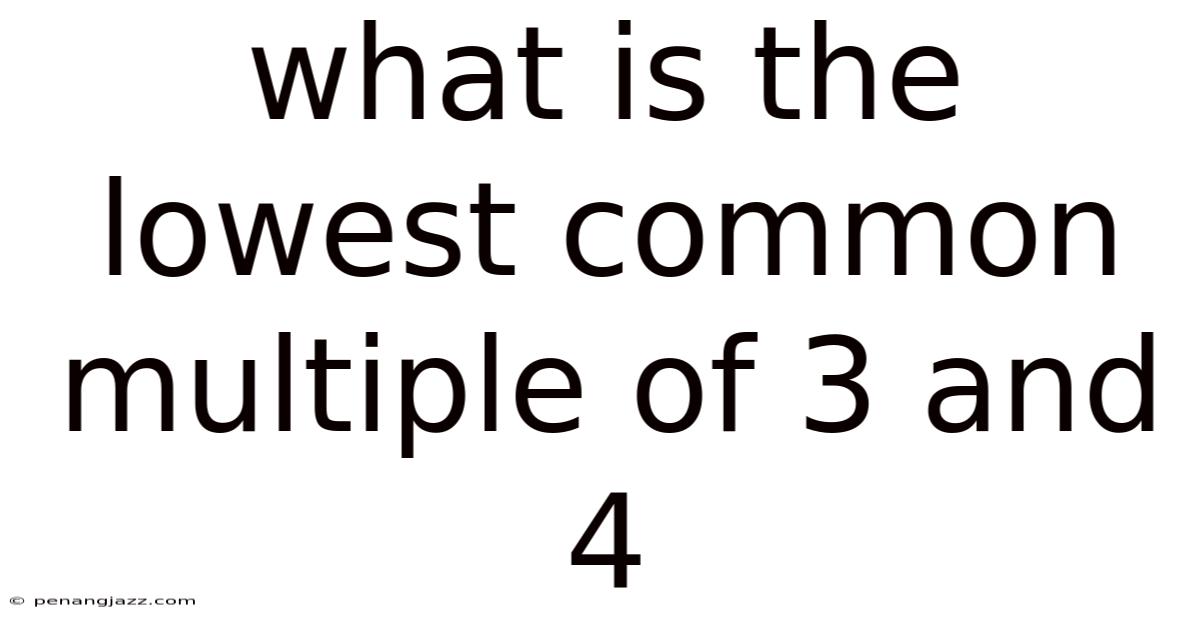
Table of Contents
The lowest common multiple (LCM) of 3 and 4 is a fundamental concept in mathematics, particularly useful in arithmetic, algebra, and number theory. Understanding how to find the LCM of numbers like 3 and 4 not only simplifies mathematical calculations but also enhances problem-solving skills. This article provides a comprehensive guide to understanding and calculating the LCM of 3 and 4, exploring various methods, real-world applications, and frequently asked questions.
Understanding the Lowest Common Multiple (LCM)
The lowest common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by each of the given numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, if we are looking for the LCM of 3 and 4, we want to find the smallest number that both 3 and 4 can divide without leaving a remainder.
The concept of LCM is closely related to the greatest common divisor (GCD), also known as the highest common factor (HCF). While LCM deals with multiples of numbers, GCD deals with factors. Both concepts are essential for simplifying fractions, solving algebraic equations, and various other mathematical problems.
Importance of Understanding LCM
Understanding and calculating the LCM is crucial for several reasons:
- Simplifying Fractions: LCM is used to find the least common denominator when adding or subtracting fractions.
- Solving Algebraic Equations: LCM helps in clearing fractions from equations, making them easier to solve.
- Real-World Applications: LCM is used in scheduling events, determining gear ratios in machines, and solving problems involving cycles.
Methods to Find the LCM of 3 and 4
There are several methods to find the LCM of 3 and 4. Each method offers a different approach and level of complexity. Here, we will explore the following methods:
- Listing Multiples
- Prime Factorization
- Division Method
1. Listing Multiples
The listing multiples method is one of the simplest ways to find the LCM, especially for small numbers like 3 and 4. This method involves listing the multiples of each number until a common multiple is found.
Steps to Find the LCM of 3 and 4 by Listing Multiples:
- List Multiples of 3:
- 3 x 1 = 3
- 3 x 2 = 6
- 3 x 3 = 9
- 3 x 4 = 12
- 3 x 5 = 15
- ...
- List Multiples of 4:
- 4 x 1 = 4
- 4 x 2 = 8
- 4 x 3 = 12
- 4 x 4 = 16
- 4 x 5 = 20
- ...
- Identify Common Multiples:
- From the lists above, we can see that 12 is a common multiple of both 3 and 4.
- Determine the Lowest Common Multiple:
- Since 12 is the smallest number that appears in both lists, the LCM of 3 and 4 is 12.
Advantages of Listing Multiples Method:
- Simple and easy to understand.
- Effective for small numbers.
Disadvantages of Listing Multiples Method:
- Time-consuming for larger numbers.
- May require writing out many multiples to find the LCM.
2. Prime Factorization
The prime factorization method involves expressing each number as a product of its prime factors and then using these prime factors to find the LCM.
Steps to Find the LCM of 3 and 4 by Prime Factorization:
- Find the Prime Factorization of 3:
- 3 is a prime number, so its prime factorization is simply 3.
- Find the Prime Factorization of 4:
- 4 = 2 x 2 = 2^2
- Identify Unique Prime Factors:
- The unique prime factors are 2 and 3.
- Determine the Highest Power of Each Prime Factor:
- The highest power of 2 is 2^2 (from the factorization of 4).
- The highest power of 3 is 3^1 (from the factorization of 3).
- Multiply the Highest Powers of All Prime Factors:
- LCM(3, 4) = 2^2 x 3^1 = 4 x 3 = 12
Advantages of Prime Factorization Method:
- Systematic and reliable.
- Useful for larger numbers.
Disadvantages of Prime Factorization Method:
- Requires knowledge of prime numbers and factorization.
- Can be more complex for very large numbers.
3. Division Method
The division method, also known as the ladder method, is a systematic way to find the LCM by dividing the numbers by their common prime factors.
Steps to Find the LCM of 3 and 4 by Division Method:
- Set Up the Division Table:
- Write the numbers 3 and 4 in a row, separated by a comma.
- Divide by Common Prime Factors:
- Since 3 and 4 do not have any common prime factors, we start by dividing each number by its smallest prime factor.
- Divide 3 by 3: 3 ÷ 3 = 1
- Divide 4 by 2: 4 ÷ 2 = 2, then divide 2 by 2: 2 ÷ 2 = 1
- Write Down the Divisors:
- The divisors are 3 and 2 (twice).
- Multiply All Divisors:
- LCM(3, 4) = 3 x 2 x 2 = 12
Advantages of Division Method:
- Systematic and organized.
- Effective for finding the LCM of multiple numbers.
Disadvantages of Division Method:
- Requires careful attention to detail.
- May be confusing for beginners.
Comparison of Methods
To summarize, here’s a comparison of the three methods discussed:
| Method | Steps | Advantages | Disadvantages |
|---|---|---|---|
| Listing Multiples | List multiples of each number until a common multiple is found. | Simple, easy to understand, effective for small numbers. | Time-consuming for larger numbers, may require writing out many multiples. |
| Prime Factorization | Express each number as a product of its prime factors, then multiply the highest powers of each factor. | Systematic, reliable, useful for larger numbers. | Requires knowledge of prime numbers and factorization, can be more complex for very large numbers. |
| Division Method | Divide the numbers by their common prime factors until all numbers are reduced to 1, then multiply the divisors. | Systematic, organized, effective for finding the LCM of multiple numbers. | Requires careful attention to detail, may be confusing for beginners. |
Real-World Applications of LCM
The concept of LCM is not just a theoretical exercise; it has several practical applications in everyday life. Here are a few examples:
1. Scheduling
Imagine you are organizing two events: a yoga class that occurs every 3 days and a book club meeting that occurs every 4 days. If both events happened today, when will they both occur on the same day again?
To solve this problem, you need to find the LCM of 3 and 4, which is 12. Therefore, both the yoga class and the book club meeting will occur on the same day again in 12 days.
2. Gear Ratios
In mechanical engineering, LCM is used to determine the gear ratios in machines. For example, if one gear has 3 teeth and another gear has 4 teeth, the LCM of 3 and 4 (which is 12) helps in designing the gear system so that both gears mesh properly after 12 rotations of the first gear and 9 rotations of the second gear.
3. Baking and Cooking
In baking and cooking, LCM can be used to adjust recipes. If a recipe calls for ingredients in ratios of 3:4, understanding the LCM helps in scaling the recipe up or down while maintaining the correct proportions.
4. Tiling
When tiling a floor or wall, LCM can help in planning the layout to minimize cuts. If you have tiles of sizes 3 inches and 4 inches, the LCM (12 inches) helps in determining the smallest square area that can be covered without cutting any tiles.
Advanced Concepts Related to LCM
While understanding the basic methods to find the LCM of 3 and 4 is essential, exploring advanced concepts can provide a deeper understanding of number theory.
LCM and GCD Relationship
The LCM and GCD of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
Where a and b are the two numbers. For example, let's find the GCD of 3 and 4:
- The factors of 3 are 1 and 3.
- The factors of 4 are 1, 2, and 4.
- The greatest common divisor (GCD) of 3 and 4 is 1.
Using the formula:
LCM(3, 4) x GCD(3, 4) = 3 x 4
LCM(3, 4) x 1 = 12
LCM(3, 4) = 12
This relationship provides an alternative method to find the LCM if the GCD is known, and vice versa.
LCM of More Than Two Numbers
The concept of LCM can be extended to more than two numbers. To find the LCM of three or more numbers, you can use the prime factorization method or the division method.
Example: Find the LCM of 3, 4, and 6
- Prime Factorization Method:
- 3 = 3
- 4 = 2^2
- 6 = 2 x 3
- LCM(3, 4, 6) = 2^2 x 3 = 4 x 3 = 12
- Division Method:
- Set up the division table: 3, 4, 6
- Divide by 2: 3, 2, 3
- Divide by 2: 3, 1, 3
- Divide by 3: 1, 1, 1
- LCM(3, 4, 6) = 2 x 2 x 3 = 12
Common Mistakes to Avoid
When finding the LCM, it's essential to avoid common mistakes that can lead to incorrect answers. Here are a few mistakes to watch out for:
- Confusing LCM with GCD: LCM is the smallest common multiple, while GCD is the greatest common divisor.
- Incorrect Prime Factorization: Ensure that the prime factorization is accurate. A mistake in the prime factorization will lead to an incorrect LCM.
- Skipping Factors: When listing multiples, make sure not to skip any factors. Skipping factors can result in missing the lowest common multiple.
- Not Reducing to Simplest Form: Ensure that the final answer is in the simplest form.
Practice Problems
To reinforce your understanding of LCM, here are a few practice problems:
- Find the LCM of 6 and 8.
- Find the LCM of 5 and 7.
- Find the LCM of 4, 6, and 9.
Solutions:
- LCM(6, 8) = 24
- LCM(5, 7) = 35
- LCM(4, 6, 9) = 36
Conclusion
The lowest common multiple (LCM) of 3 and 4 is 12. Understanding how to find the LCM using methods like listing multiples, prime factorization, and the division method is crucial for various mathematical and real-world applications. By mastering these techniques and avoiding common mistakes, you can confidently solve problems involving LCM and enhance your problem-solving skills. The LCM is not just a mathematical concept; it's a tool that simplifies complex calculations and provides insights into the relationships between numbers.
Latest Posts
Latest Posts
-
The General Formula For An Acid Is
Nov 21, 2025
-
What Type Of Bacteria Convert Ammonia To Nitrites And Nitrates
Nov 21, 2025
-
One Sample Z Test For Proportions
Nov 21, 2025
-
How To Find The Beat Frequency
Nov 21, 2025
-
Before Entering The Krebs Cycle Pyruvate Is Converted To
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.