What Is The Lcm Of 4 And 7
penangjazz
Nov 06, 2025 · 11 min read
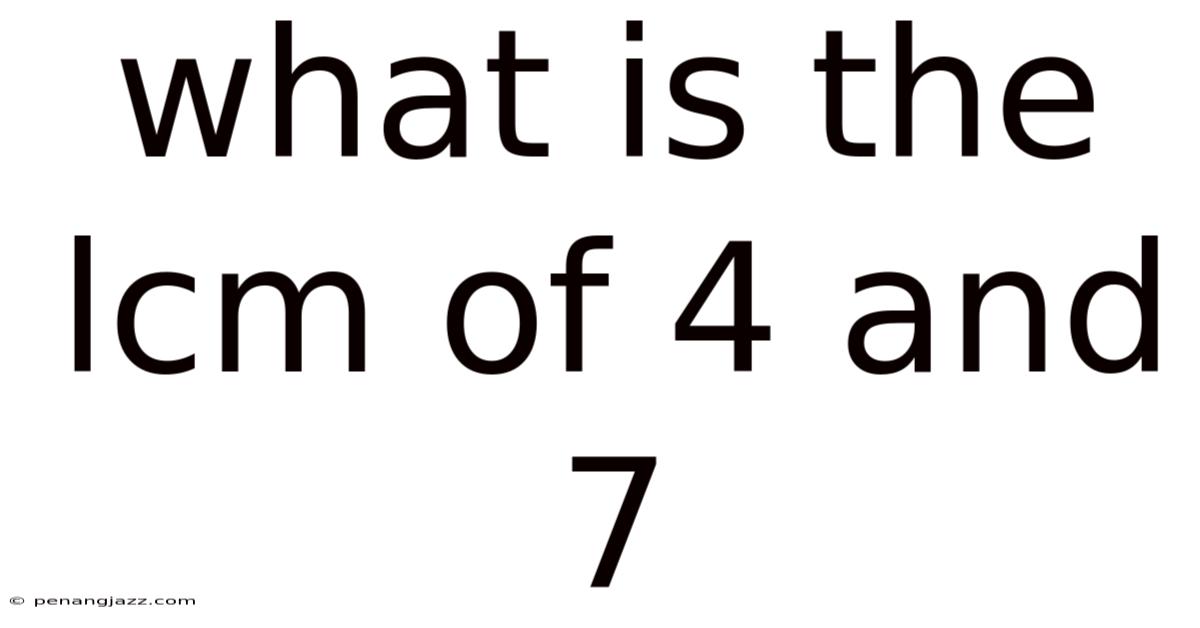
Table of Contents
The Least Common Multiple (LCM) of 4 and 7 might seem like a simple arithmetic problem, but understanding the concept behind it opens doors to a broader understanding of number theory and its applications in everyday life. From scheduling tasks to understanding musical harmonies, the LCM is a fundamental tool. Let's dive into what it is, how to calculate it, and why it matters.
Understanding the Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of those numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. It's a core concept in number theory, often used in simplifying fractions, solving algebraic equations, and understanding cyclical patterns.
To fully grasp the concept, consider these related terms:
- Multiple: A multiple of a number is the result of multiplying that number by an integer. For example, multiples of 4 are 4, 8, 12, 16, and so on.
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of each of those numbers. For example, common multiples of 4 and 7 include 28, 56, and 84.
- Least: The "least" specifies that we are looking for the smallest of the common multiples.
Methods to Calculate the LCM of 4 and 7
Several methods can be used to find the LCM of two numbers. Here, we will explore the most common and effective techniques:
- Listing Multiples
- Prime Factorization
- Using the Greatest Common Divisor (GCD)
1. Listing Multiples
This method involves listing the multiples of each number until you find a common multiple. The smallest common multiple is the LCM.
Step-by-step for 4 and 7:
- List multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
- List multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, ...
By comparing the lists, we find that the smallest multiple common to both 4 and 7 is 28. Therefore, the LCM of 4 and 7 is 28.
This method is straightforward and easy to understand, making it ideal for small numbers. However, it can become cumbersome and time-consuming for larger numbers.
2. Prime Factorization
This method breaks down each number into its prime factors. The LCM is then found by multiplying the highest powers of all prime factors involved.
Step-by-step for 4 and 7:
-
Prime Factorization of 4:
- 4 = 2 x 2 = 2<sup>2</sup>
-
Prime Factorization of 7:
- 7 = 7<sup>1</sup> (7 is a prime number)
-
Identify all unique prime factors:
- The unique prime factors are 2 and 7.
-
Take the highest power of each prime factor:
- The highest power of 2 is 2<sup>2</sup>.
- The highest power of 7 is 7<sup>1</sup>.
-
Multiply these highest powers together:
- LCM(4, 7) = 2<sup>2</sup> x 7<sup>1</sup> = 4 x 7 = 28
Therefore, using the prime factorization method, the LCM of 4 and 7 is 28. This method is particularly useful for larger numbers, as it simplifies the process by focusing on prime factors.
3. Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF), is the largest positive integer that divides two or more numbers without leaving a remainder. There's a relationship between the LCM and GCD of two numbers:
LCM(a, b) = (|a| * |b|) / GCD(a, b)
In other words, the LCM of two numbers can be found by multiplying the absolute values of the numbers and dividing by their GCD.
Step-by-step for 4 and 7:
-
Find the GCD of 4 and 7:
- The factors of 4 are 1, 2, and 4.
- The factors of 7 are 1 and 7.
- The only common factor is 1, so GCD(4, 7) = 1.
-
Use the formula to find the LCM:
- LCM(4, 7) = (4 * 7) / GCD(4, 7) = (4 * 7) / 1 = 28
Therefore, using the GCD method, the LCM of 4 and 7 is 28. This method is useful when you already know the GCD or can find it easily.
Why is LCM Important?
The Least Common Multiple is not just an abstract mathematical concept; it has practical applications in various fields. Understanding and calculating the LCM can help in solving real-world problems.
1. Simplifying Fractions
In mathematics, the LCM is often used when adding or subtracting fractions with different denominators. To add or subtract such fractions, you need to find a common denominator, which is the LCM of the original denominators.
Example:
Suppose you want to add 1/4 and 1/7. The denominators are 4 and 7. We already know that the LCM of 4 and 7 is 28. Therefore, we can rewrite the fractions with the common denominator of 28:
- 1/4 = 7/28
- 1/7 = 4/28
Now, adding the fractions is straightforward:
- 7/28 + 4/28 = 11/28
2. Scheduling and Planning
The LCM is useful in scheduling events that occur at different intervals.
Example:
Imagine you have two tasks:
- Task A needs to be done every 4 days.
- Task B needs to be done every 7 days.
If both tasks are done today, when will they both need to be done again on the same day? The answer is the LCM of 4 and 7, which is 28. So, in 28 days, both tasks will need to be done again on the same day. This principle can be applied to scheduling meetings, maintenance tasks, or any other recurring event.
3. Gear Ratios
In mechanical engineering, the LCM is used to determine the number of rotations needed for gears to align again.
Example:
Consider two gears:
- Gear X has 4 teeth.
- Gear Y has 7 teeth.
How many rotations will each gear make before they return to their starting positions simultaneously? The answer lies in the LCM. Gear X will make 7 rotations (28/4), and Gear Y will make 4 rotations (28/7) before they align again.
4. Music Theory
In music theory, the LCM can be used to understand the relationship between different rhythmic patterns.
Example:
Suppose one musical phrase repeats every 4 beats, and another repeats every 7 beats. The LCM (28) tells you that after 28 beats, both phrases will align again. This helps in understanding complex musical structures and harmonies.
5. Real-World Applications
The LCM finds its applications in diverse fields, including:
- Manufacturing: Optimizing production cycles of different machines.
- Transportation: Coordinating schedules of buses or trains with varying frequencies.
- Computer Science: Scheduling tasks in operating systems or databases.
Common Mistakes to Avoid
When calculating the LCM, there are several common mistakes that individuals often make. Awareness of these pitfalls can help prevent errors and ensure accurate results.
1. Confusing LCM with GCD
One of the most common mistakes is confusing the Least Common Multiple (LCM) with the Greatest Common Divisor (GCD). Remember that the LCM is the smallest multiple that two numbers share, while the GCD is the largest divisor they share. Using the wrong concept can lead to completely incorrect answers.
2. Incorrect Prime Factorization
The prime factorization method is powerful, but errors in factoring numbers into primes can lead to an incorrect LCM. Ensure that you accurately break down each number into its prime factors.
Example of an Incorrect Factorization:
Suppose you incorrectly factor 4 as 2 x 3 instead of 2 x 2. This will lead to an incorrect LCM when combined with the prime factors of other numbers.
3. Missing Common Multiples
When listing multiples, it's easy to miss the least common multiple, especially if you stop listing multiples too early. Always ensure you list enough multiples to find the smallest one they have in common.
4. Arithmetic Errors
Simple arithmetic errors can occur when multiplying or dividing during the LCM calculation, particularly when using the GCD method. Double-check your calculations to avoid these mistakes.
5. Not Simplifying
Sometimes, after finding a common multiple, individuals may not realize that it is not the least common multiple. Always ensure that the common multiple you have found is the smallest possible.
Advanced Concepts Related to LCM
While understanding the basic concept of LCM is crucial, exploring advanced concepts can deepen your knowledge and broaden its applications.
1. LCM of More Than Two Numbers
The LCM can be extended to more than two numbers. To find the LCM of three or more numbers, you can use the prime factorization method or a step-by-step approach.
Example:
Find the LCM of 4, 7, and 10.
-
Prime Factorization:
- 4 = 2<sup>2</sup>
- 7 = 7<sup>1</sup>
- 10 = 2<sup>1</sup> x 5<sup>1</sup>
-
Identify unique prime factors and their highest powers:
- 2<sup>2</sup>, 5<sup>1</sup>, 7<sup>1</sup>
-
Multiply these together:
- LCM(4, 7, 10) = 2<sup>2</sup> x 5<sup>1</sup> x 7<sup>1</sup> = 4 x 5 x 7 = 140
Therefore, the LCM of 4, 7, and 10 is 140.
2. Relationship Between LCM and GCD
The relationship between the LCM and GCD is a fundamental concept in number theory. For any two positive integers a and b:
LCM(a, b) * GCD(a, b) = |a * b|
This relationship provides a way to find the LCM if you know the GCD, and vice versa. It also highlights the interconnectedness of these two concepts.
3. Applications in Abstract Algebra
In abstract algebra, the concept of LCM extends to polynomials and other algebraic structures. The LCM of two polynomials is the polynomial of the smallest degree that is divisible by both polynomials. This concept is used in various algebraic manipulations and solving polynomial equations.
4. Modular Arithmetic
The LCM is also related to modular arithmetic, particularly in finding solutions to systems of congruences. Understanding the LCM can help in determining when solutions exist and in finding those solutions.
Practical Examples and Exercises
To solidify your understanding of the LCM, let’s go through a few practical examples and exercises.
Example 1: Tiling a Floor
Suppose you want to tile a rectangular floor using square tiles. You have two types of tiles:
- Tile A: 4 inches by 4 inches
- Tile B: 7 inches by 7 inches
What is the smallest square floor that can be tiled completely using either Tile A or Tile B without cutting any tiles?
Solution:
The side length of the square floor must be a multiple of both 4 and 7. Therefore, we need to find the LCM of 4 and 7, which is 28. The smallest square floor that can be tiled completely is 28 inches by 28 inches.
Example 2: Synchronizing Lights
Two lights blink at different intervals:
- Light X blinks every 4 seconds.
- Light Y blinks every 7 seconds.
If they blink together now, how many seconds will pass before they blink together again?
Solution:
We need to find the LCM of 4 and 7, which is 28. Therefore, the lights will blink together again after 28 seconds.
Exercise 1: Finding LCM
Find the LCM of the following pairs of numbers using the prime factorization method:
- 6 and 8
- 12 and 15
- 9 and 21
Exercise 2: Scheduling Tasks
You have two tasks to complete:
- Task A: Needs to be done every 6 days.
- Task B: Needs to be done every 9 days.
If you do both tasks today, how many days will pass before you need to do both tasks on the same day again?
Exercise 3: Gear Rotations
Two gears have the following number of teeth:
- Gear P: 10 teeth
- Gear Q: 12 teeth
How many rotations will each gear make before they return to their starting positions simultaneously?
Conclusion
Finding the Least Common Multiple (LCM) of 4 and 7 is a fundamental exercise in number theory that showcases the importance of understanding multiples and prime factorization. The LCM of 4 and 7 is 28, a result obtained through listing multiples, prime factorization, or using the relationship with the Greatest Common Divisor (GCD).
The practical applications of the LCM extend to various real-world scenarios, including simplifying fractions, scheduling tasks, understanding gear ratios, and analyzing musical rhythms. By mastering the concept of the LCM, you can enhance your problem-solving skills and gain a deeper appreciation for mathematics in everyday life. Avoiding common mistakes and exploring advanced concepts further solidifies this understanding, making you proficient in applying the LCM to diverse and complex situations.
Latest Posts
Latest Posts
-
Applications Of Exponential And Logarithmic Functions
Nov 06, 2025
-
Graphs That Represent Y As A Function Of X
Nov 06, 2025
-
What Is The Most Basic Unit Of Life
Nov 06, 2025
-
Calculate By Changing To Polar Coordinates
Nov 06, 2025
-
Which Regression Equation Best Fits The Data
Nov 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.