What Is 4.5 As A Fraction
penangjazz
Nov 17, 2025 · 9 min read
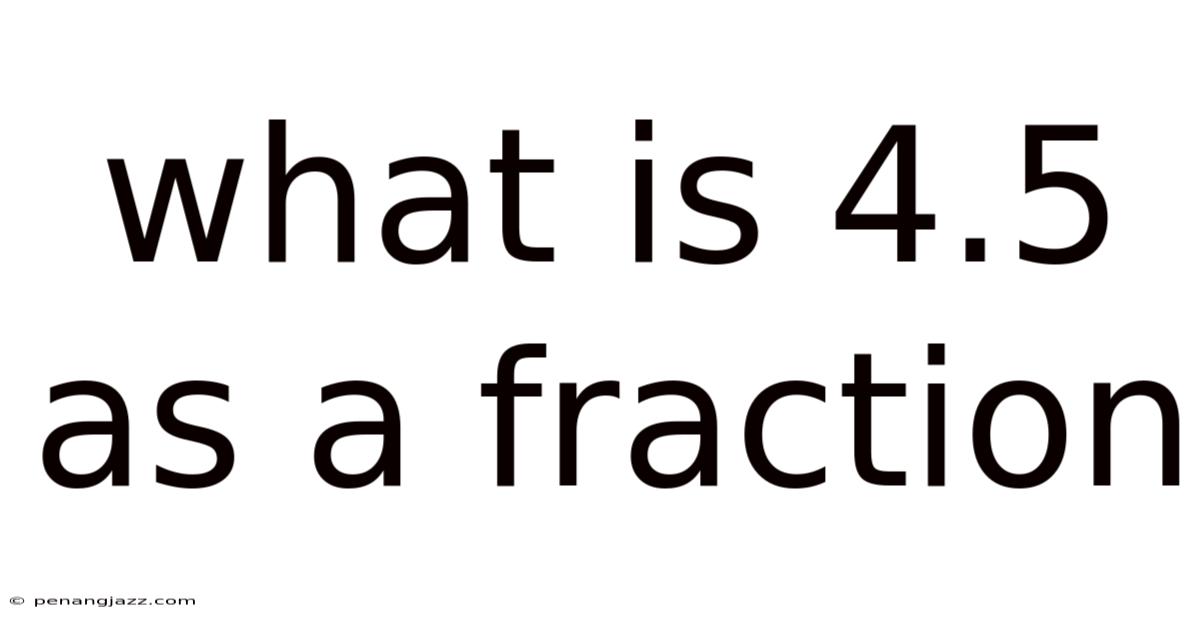
Table of Contents
Turning a decimal into a fraction can feel like unlocking a secret code, especially when dealing with numbers like 4.5. This number represents a quantity that's more than just whole units; it includes a precise part of a unit, making it a mixed number waiting to be expressed as a fraction.
Understanding Decimals and Fractions
Before diving into converting 4.5, it’s crucial to understand the relationship between decimals and fractions. Both are ways to represent numbers that are not whole numbers. A decimal is based on a power of 10, with each digit after the decimal point representing tenths, hundredths, thousandths, and so on. A fraction, on the other hand, represents a part of a whole, with a numerator (the top number) indicating how many parts we have and a denominator (the bottom number) indicating how many parts the whole is divided into.
The Basics: Converting Decimals to Fractions
To convert a decimal to a fraction, you follow a few simple steps:
- Identify the decimal: In our case, it’s 4.5.
- Write the decimal as a fraction over 1: Think of 4.5 as 4.5/1.
- Multiply to remove the decimal: Since we have one digit after the decimal point, we multiply both the numerator and the denominator by 10. This gives us 45/10.
- Simplify the fraction: Now, we simplify 45/10 to its simplest form.
Step-by-Step Conversion of 4.5 to a Fraction
Let's walk through the conversion process for 4.5 step by step:
-
Start with the decimal: We begin with 4.5, which we want to convert into a fraction.
-
Express as a fraction over 1: We write 4.5 as 4.5/1. This doesn't change the value but sets us up for the next step.
-
Eliminate the decimal point: To get rid of the decimal, we multiply both the numerator and the denominator by 10. This gives us:
(4. 5 * 10) / (1 * 10) = 45/10
-
Simplify the fraction: The fraction 45/10 can be simplified. Both 45 and 10 are divisible by 5. So, we divide both the numerator and the denominator by 5:
45 ÷ 5 = 9 10 ÷ 5 = 2
This simplifies our fraction to 9/2.
-
Final fraction: Therefore, 4.5 as a fraction in its simplest form is 9/2. This is an improper fraction because the numerator is greater than the denominator.
Converting an Improper Fraction to a Mixed Number
Sometimes, it's more useful to express an improper fraction (where the numerator is greater than the denominator) as a mixed number (a whole number and a fraction). Here's how to convert 9/2 into a mixed number:
- Divide the numerator by the denominator: Divide 9 by 2.
- 9 ÷ 2 = 4 with a remainder of 1.
- Write the mixed number: The whole number part is the quotient (4), and the remainder (1) becomes the numerator of the fractional part. The denominator stays the same (2).
- So, 9/2 as a mixed number is 4 1/2.
Thus, 4.5 can also be expressed as the mixed number 4 1/2.
Why Does This Method Work?
The method works because we're essentially scaling the number to remove the decimal part without changing its value. Multiplying by powers of 10 (10, 100, 1000, etc.) moves the decimal point to the right, effectively turning the decimal into a whole number. When we multiply both the numerator and the denominator by the same number, we’re only multiplying the fraction by 1, which preserves its value.
Common Mistakes to Avoid
- Forgetting to multiply the denominator: One common mistake is only multiplying the numerator by 10, 100, or 1000 to remove the decimal, forgetting that you must do the same to the denominator to maintain the fraction's value.
- Not simplifying the fraction: Always simplify the fraction to its simplest form. A fraction like 45/10 is correct but not in its simplest form.
- Incorrect division: When converting an improper fraction to a mixed number, make sure you perform the division correctly. The remainder becomes the new numerator, and the denominator stays the same.
Real-World Applications
Understanding how to convert decimals to fractions is useful in many real-world situations:
- Cooking: Recipes often use fractions, but measurements might be in decimal form. Converting allows you to measure ingredients accurately.
- Construction: Building and construction often require precise measurements. Being able to convert between decimals and fractions helps ensure accuracy in cutting materials and fitting pieces together.
- Finance: In finance, interest rates and percentage increases might be given as decimals. Converting these to fractions can help in understanding the actual proportion of the whole.
- Education: This skill is fundamental in mathematics and is often tested in standardized tests and everyday math problems.
Examples and Practice Problems
To solidify your understanding, let's go through a few examples and practice problems.
Example 1: Convert 2.75 to a fraction
- Start with 2.75/1.
- Multiply both numerator and denominator by 100 (since there are two digits after the decimal point): (2.75 * 100) / (1 * 100) = 275/100
- Simplify: Both 275 and 100 are divisible by 25.
- 275 ÷ 25 = 11
- 100 ÷ 25 = 4
- The simplified fraction is 11/4.
- As a mixed number: 11 ÷ 4 = 2 with a remainder of 3. So, the mixed number is 2 3/4.
Example 2: Convert 0.6 to a fraction
- Start with 0.6/1.
- Multiply both numerator and denominator by 10: (0.6 * 10) / (1 * 10) = 6/10
- Simplify: Both 6 and 10 are divisible by 2.
- 6 ÷ 2 = 3
- 10 ÷ 2 = 5
- The simplified fraction is 3/5.
Practice Problems:
- Convert 1.25 to a fraction.
- Convert 3.8 to a fraction.
- Convert 0.15 to a fraction.
- Convert 6.4 to a fraction.
Advanced Conversions and Special Cases
Sometimes, you might encounter repeating decimals or more complex numbers. Here are some tips for handling these situations:
- Repeating decimals: Converting repeating decimals to fractions involves a bit more algebra. For example, to convert 0.333... to a fraction, you can set x = 0.333..., then 10x = 3.333.... Subtracting the first equation from the second gives 9x = 3, so x = 3/9, which simplifies to 1/3.
- Complex decimals: For decimals with many digits after the decimal point, the process remains the same. Just remember to multiply by the correct power of 10 to remove the decimal.
The Mathematical Explanation Behind Decimal to Fraction Conversion
The conversion of a decimal to a fraction is based on the fundamental principles of place value in the decimal system. Each position to the right of the decimal point represents a fraction with a denominator that is a power of 10. The first digit after the decimal point represents tenths (1/10), the second digit represents hundredths (1/100), the third digit represents thousandths (1/1000), and so on.
When we convert a decimal to a fraction, we are essentially re-expressing the decimal as a sum of fractions with denominators that are powers of 10. For example, the decimal 0.75 can be thought of as:
0.75 = 7/10 + 5/100
To combine these fractions into a single fraction, we need a common denominator. In this case, the common denominator is 100:
0.75 = 70/100 + 5/100 = 75/100
This fraction can then be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25:
75/100 = 3/4
This process works for any decimal, regardless of the number of digits after the decimal point. The key is to identify the place value of the rightmost digit and use that as the denominator of the initial fraction.
Converting Decimals to Fractions
The general formula for converting a decimal to a fraction can be expressed as follows:
Given a decimal D with n digits after the decimal point, the equivalent fraction F can be written as:
F = D × 10ⁿ / 10ⁿ
Where:
- D is the decimal number.
- n is the number of digits after the decimal point.
For example, if D = 0.125, then n = 3. Applying the formula:
F = 0.125 × 10³/ 10³ = 125/1000
This fraction can then be simplified to its lowest terms.
Converting Mixed Decimals to Fractions
A mixed decimal consists of a whole number part and a decimal part. To convert a mixed decimal to a fraction, we first convert the decimal part to a fraction, and then add it to the whole number part.
For example, consider the mixed decimal 3.25. The whole number part is 3, and the decimal part is 0.25. We convert the decimal part to a fraction as follows:
0.25 = 25/100 = 1/4
Now, we add the fraction to the whole number:
3 + 1/4 = 12/4 + 1/4 = 13/4
So, the mixed decimal 3.25 is equivalent to the fraction 13/4.
The Importance of Simplifying Fractions
Simplifying fractions is an essential step in the conversion process. A fraction is in its simplest form when the numerator and the denominator have no common factors other than 1. Simplifying fractions makes them easier to work with and understand.
For example, the fraction 75/100 is not in its simplest form because both 75 and 100 have common factors (e.g., 5, 25). To simplify this fraction, we divide both the numerator and the denominator by their greatest common divisor (GCD), which is 25:
75/100 = (75 ÷ 25) / (100 ÷ 25) = 3/4
The simplified fraction 3/4 is now in its simplest form because 3 and 4 have no common factors other than 1.
Converting Fractions Back to Decimals
It's also important to understand how to convert fractions back to decimals, as this can be useful for checking your work or for situations where decimals are preferred.
To convert a fraction to a decimal, you simply divide the numerator by the denominator. For example, to convert the fraction 3/4 to a decimal, you divide 3 by 4:
3 ÷ 4 = 0.75
The result is the decimal equivalent of the fraction.
The Role of Place Value
Place value plays a crucial role in understanding and converting between decimals and fractions. In the decimal system, each digit has a specific place value that is a power of 10. The place values to the right of the decimal point are:
- Tenths (10⁻¹ = 0.1)
- Hundredths (10⁻² = 0.01)
- Thousandths (10⁻³ = 0.001)
- Ten-thousandths (10⁻⁴ = 0.0001)
- And so on...
Understanding these place values helps in converting decimals to fractions and vice versa.
Conclusion: Mastering Decimal to Fraction Conversions
Converting decimals to fractions is a fundamental skill with wide-ranging applications in everyday life and various professional fields. By understanding the basic principles and following the step-by-step methods outlined in this guide, you can confidently convert any decimal to its equivalent fraction. Remember to simplify the fraction to its lowest terms and to convert improper fractions to mixed numbers when appropriate.
With practice and a solid understanding of the underlying mathematical concepts, you’ll be able to convert decimals to fractions with ease and accuracy.
Latest Posts
Latest Posts
-
What Is The Domain Of Tangent
Nov 17, 2025
-
Is Hydrogen Bonding Stronger Than Dipole Dipole
Nov 17, 2025
-
3 8 Or 5 16 Larger
Nov 17, 2025
-
How Do You Do Distributive Property
Nov 17, 2025
-
Area Of Non Right Angled Triangles
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 4.5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.