What Is 10 Percent Of 12
penangjazz
Nov 24, 2025 · 5 min read
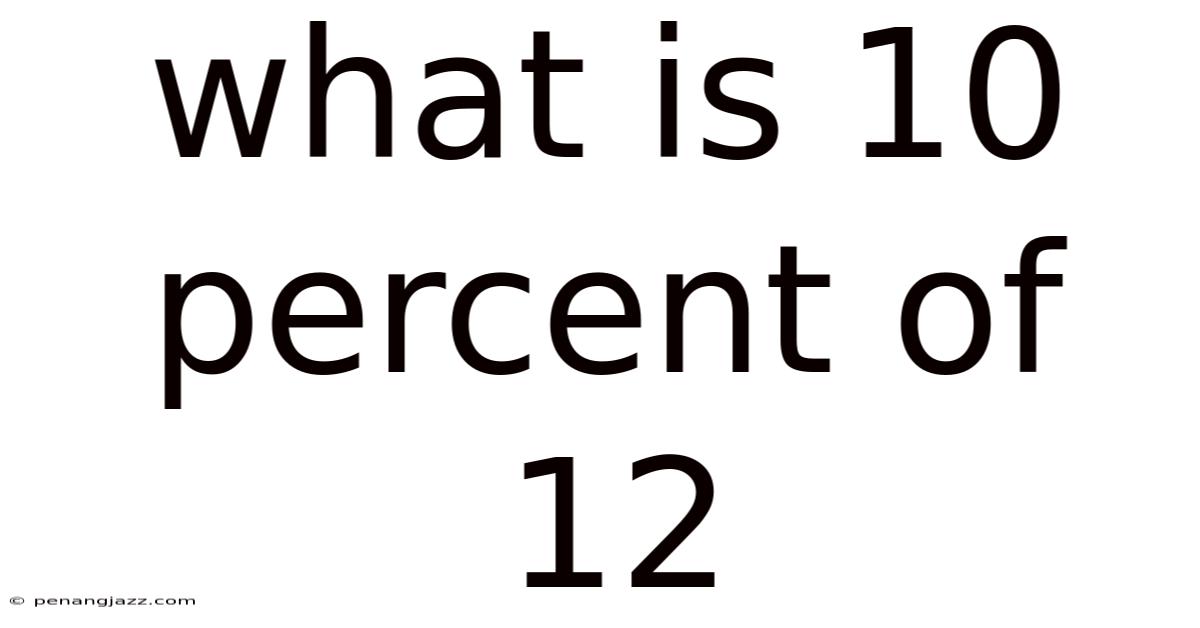
Table of Contents
Calculating percentages is a fundamental skill applicable across various aspects of life, from figuring out discounts while shopping to understanding statistical data. When faced with the question, "What is 10 percent of 12?", the solution is relatively straightforward but understanding the underlying principles can enhance one's mathematical proficiency.
The Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred". Therefore, 10 percent (10%) is equivalent to 10/100, which can be simplified to 1/10 or 0.1 in decimal form. Understanding this basic definition is crucial for performing percentage calculations accurately.
Methods to Calculate 10 Percent of 12
There are several methods to calculate 10 percent of 12. Here, we explore three common approaches: the fraction method, the decimal method, and the proportional method.
1. The Fraction Method
The fraction method involves converting the percentage into a fraction and then multiplying it by the whole number. For 10 percent, the fraction is 10/100, which simplifies to 1/10. The calculation then becomes:
(1/10) * 12 = 12/10 = 1.2
2. The Decimal Method
The decimal method is perhaps the most straightforward and commonly used approach. To use this method, convert the percentage to a decimal by dividing it by 100. For 10 percent, this conversion results in 0.1. The calculation is then a simple multiplication:
0. 1 * 12 = 1.2
3. The Proportional Method
The proportional method involves setting up a proportion to find the unknown value. If 12 represents 100%, then we want to find what value represents 10%. The proportion can be written as:
10/100 = x/12
To solve for x, cross-multiply:
100 * x = 10 * 12
100 * x = 120
x = 120 / 100
x = 1.2
Step-by-Step Calculation
To further clarify, let's break down the calculation using the decimal method, which is widely regarded as the simplest.
-
Step 1: Convert the Percentage to a Decimal
Divide 10 by 100 to convert 10% to a decimal:
10 / 100 = 0.1 -
Step 2: Multiply the Decimal by the Whole Number
Multiply the decimal (0.1) by the whole number (12):
0. 1 * 12 = 1.2
Therefore, 10 percent of 12 is 1.2.
Real-World Applications
Understanding how to calculate percentages is valuable in numerous real-world scenarios. Here are a few examples:
- Shopping Discounts: When shopping, discounts are often expressed as percentages. For example, a 10% discount on an item priced at $12 means you save $1.20. The new price would be $12 - $1.20 = $10.80.
- Financial Planning: In finance, calculating percentages is essential for understanding investment returns, interest rates, and budget allocations. For instance, if you allocate 10% of your $1200 monthly income to savings, you would save $120 each month.
- Academic Assessments: Teachers often use percentages to grade assignments and exams. If a student scores 12 out of 120 on a test, their score can be expressed as a percentage: (12/120) * 100 = 10%.
- Statistical Analysis: Percentages are used to interpret data in statistical analysis, such as market share, population growth, and survey results. If a survey of 1200 people shows that 120 prefer a particular brand, this represents 10% of the surveyed population.
Common Mistakes and How to Avoid Them
While calculating percentages is generally straightforward, some common mistakes can lead to incorrect answers. Here are a few pitfalls to avoid:
- Forgetting to Convert the Percentage to a Decimal or Fraction: One of the most common errors is forgetting to convert the percentage to its decimal or fraction form before multiplying. Always divide the percentage by 100 to get the decimal equivalent.
- Misunderstanding the Base Number: Ensure you are applying the percentage to the correct base number. For instance, if calculating a discount, apply the percentage to the original price, not a reduced price.
- Incorrectly Setting up Proportions: When using the proportional method, ensure that the proportion is set up correctly. The ratios must be consistent (e.g., percentage/100 = part/whole).
- Rounding Errors: Be cautious with rounding, especially in multi-step calculations. Rounding too early can lead to significant inaccuracies in the final result.
Advanced Percentage Calculations
Beyond simple percentage calculations, there are more advanced concepts that build upon these fundamental skills:
-
Percentage Increase and Decrease: Calculating the percentage increase or decrease between two values involves finding the difference between the values, dividing by the original value, and then multiplying by 100.
-
Compound Interest: Compound interest involves earning interest not only on the initial principal but also on the accumulated interest from previous periods. The formula for compound interest is:
A = P(1 + r/n)^(nt)Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
-
Weighted Averages: A weighted average is an average in which each quantity to be averaged is assigned a weight. These weights determine the relative importance of each quantity in the average.
The Significance of Understanding Percentages
Understanding percentages is not just an academic exercise; it is a crucial life skill. The ability to calculate percentages accurately empowers individuals to make informed decisions in various contexts, from managing personal finances to evaluating business opportunities. Whether you are a student, a professional, or a consumer, a solid grasp of percentage calculations will undoubtedly prove beneficial.
Practical Exercises
To reinforce your understanding, here are a few practical exercises:
-
Calculate 10% of 50:
- Decimal Method: 0.1 * 50 = 5
- Fraction Method: (1/10) * 50 = 5
-
Calculate 10% of 250:
- Decimal Method: 0.1 * 250 = 25
- Fraction Method: (1/10) * 250 = 25
-
Calculate 10% of 1500:
- Decimal Method: 0.1 * 1500 = 150
- Fraction Method: (1/10) * 1500 = 150
Conclusion
In summary, calculating 10 percent of 12 is a straightforward mathematical problem with significant real-world applications. By understanding the basic principles of percentages and employing methods such as the fraction, decimal, or proportional approach, anyone can accurately determine that 10% of 12 is 1.2. Mastering these fundamental skills not only enhances mathematical proficiency but also empowers individuals to make informed decisions in various aspects of life. From calculating discounts while shopping to understanding financial data, the ability to work with percentages is an invaluable asset.
Latest Posts
Latest Posts
-
How To Factor Polynomial With Fraction Exponents
Nov 24, 2025
-
How To Calculate Coupling Constant Nmr
Nov 24, 2025
-
How To Solve Linear Equations With Fractions
Nov 24, 2025
-
How To Find The Heat Capacity Of A Calorimeter
Nov 24, 2025
-
Principles Of Verbal And Nonverbal Communication
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.