Value Of R In Pv Nrt
penangjazz
Nov 28, 2025 · 10 min read
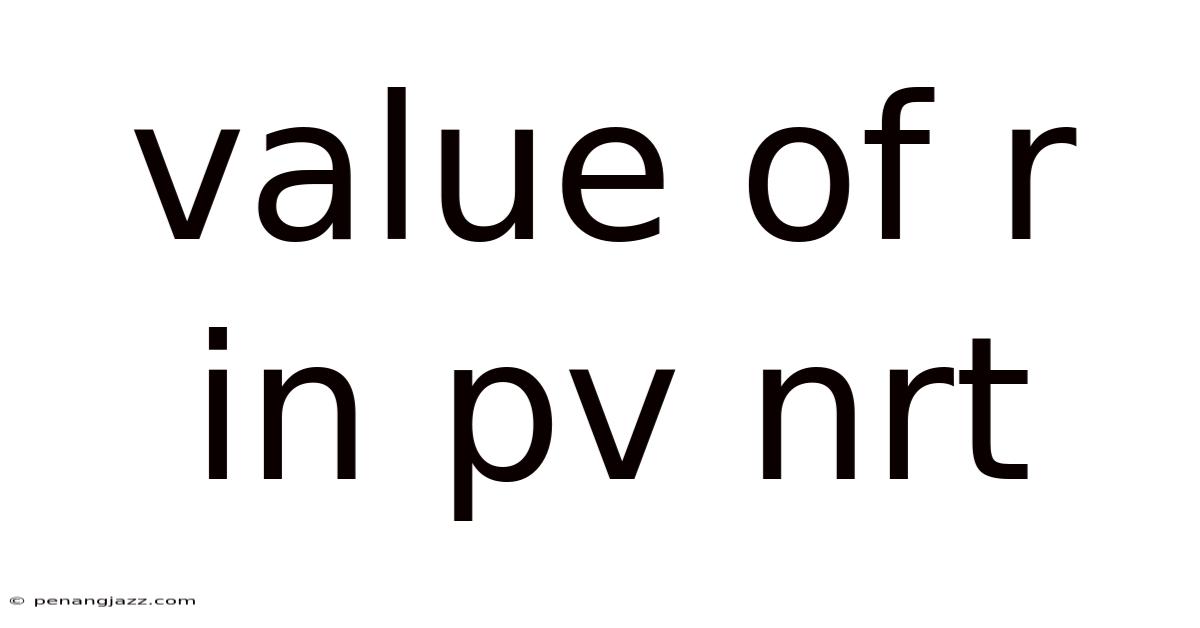
Table of Contents
In the world of chemistry and physics, the ideal gas law, expressed as PV = nRT, stands as a cornerstone for understanding the behavior of gases under various conditions. While each component of this equation holds significance, the gas constant 'R' is particularly noteworthy. This article delves into the profound value of R in PV = nRT, exploring its origins, significance, applications, and its role in bridging different units and scales in scientific calculations.
Understanding the Ideal Gas Law: PV = nRT
The ideal gas law is a simplified model that describes the relationship between pressure (P), volume (V), number of moles (n), and temperature (T) of an ideal gas. An ideal gas is a theoretical gas composed of randomly moving point particles that do not interact except when they collide elastically. Although no gas is perfectly ideal, many gases approximate ideal behavior under certain conditions, such as high temperature and low pressure.
- P (Pressure): The force exerted per unit area by the gas on the walls of its container, typically measured in Pascals (Pa), atmospheres (atm), or bars.
- V (Volume): The space occupied by the gas, usually measured in liters (L) or cubic meters (m³).
- n (Number of Moles): The amount of substance, representing the number of gas particles, measured in moles (mol).
- T (Temperature): The average kinetic energy of the gas particles, measured in Kelvin (K).
- R (Ideal Gas Constant): The proportionality constant that relates the energy scale to the temperature scale, connecting the units of pressure, volume, moles, and temperature.
The Significance of R: The Ideal Gas Constant
The ideal gas constant (R) is a fundamental physical constant that appears in the ideal gas law. It represents the amount of energy required to raise the temperature of one mole of an ideal gas by one Kelvin under constant pressure and volume conditions. More broadly, it serves as a bridge between the macroscopic properties of a gas (P, V, T) and the microscopic quantity of the gas (n).
Numerical Value and Units of R
The value of R depends on the units used for pressure, volume, and temperature. The most common values include:
- R = 0.0821 L·atm/mol·K: When pressure is in atmospheres (atm), volume is in liters (L), and temperature is in Kelvin (K).
- R = 8.314 J/mol·K: When pressure is in Pascals (Pa), volume is in cubic meters (m³), and temperature is in Kelvin (K). This value is particularly important because it expresses R in SI units.
- R = 1.987 cal/mol·K: When energy is measured in calories (cal), which is frequently used in chemical thermodynamics.
Origin and Derivation of R
The value of R can be derived from experimental observations and the work of scientists like Robert Boyle, Jacques Charles, and Amedeo Avogadro.
- Boyle's Law: States that for a fixed amount of gas at constant temperature, the pressure and volume are inversely proportional (P ∝ 1/V).
- Charles's Law: States that for a fixed amount of gas at constant pressure, the volume is directly proportional to the temperature (V ∝ T).
- Avogadro's Principle: States that equal volumes of all gases at the same temperature and pressure contain the same number of molecules. One mole of any gas at standard temperature and pressure (STP, 0°C or 273.15 K and 1 atm) occupies approximately 22.4 liters.
Using Avogadro's principle, we can calculate R:
R = (P * V) / (n * T) = (1 atm * 22.4 L) / (1 mol * 273.15 K) ≈ 0.0821 L·atm/mol·K
Similarly, using SI units:
R = (101325 Pa * 0.0224 m³) / (1 mol * 273.15 K) ≈ 8.314 J/mol·K
Importance of Using Correct Units with R
The value of R must be selected to match the units of pressure, volume, and temperature used in the problem. Inconsistent units will result in incorrect calculations. For example:
- If pressure is given in kPa and volume is in liters, converting to atm and using R = 0.0821 L·atm/mol·K or converting to m³ and Pascals and using R = 8.314 J/mol·K is necessary.
- If temperature is given in Celsius, it must be converted to Kelvin before using the ideal gas law.
Applications of R in Various Fields
The ideal gas constant (R) finds extensive applications across various scientific and engineering disciplines. Its ability to link the macroscopic and microscopic properties of gases makes it invaluable for both theoretical and practical applications.
Chemistry
In chemistry, the ideal gas law and, by extension, the value of R, are indispensable for:
- Stoichiometry of Gaseous Reactions: Calculating the volumes of gases produced or consumed in chemical reactions.
- Determining Molar Mass: Using the ideal gas law to find the molar mass of a gas by measuring its pressure, volume, and temperature.
- Gas Mixtures: Analyzing the behavior of gas mixtures, such as air, and determining the partial pressures of individual components.
- Chemical Thermodynamics: Calculating changes in energy, enthalpy, and entropy in reactions involving gases.
Physics
In physics, R is crucial for understanding the behavior of gases and is used in:
- Thermodynamics: Describing thermodynamic processes such as isothermal, adiabatic, and isobaric processes.
- Kinetic Theory of Gases: Relating the macroscopic properties of a gas to the average kinetic energy of its molecules.
- Statistical Mechanics: Calculating the properties of gases based on the statistical behavior of large numbers of particles.
- Meteorology: Modeling atmospheric conditions, predicting weather patterns, and understanding climate change.
Engineering
Engineers rely on the ideal gas law and the value of R for designing and optimizing various systems:
- Chemical Engineering: Designing reactors, distillation columns, and other equipment for chemical processes.
- Mechanical Engineering: Analyzing the performance of engines, turbines, and compressors.
- Aerospace Engineering: Modeling the behavior of gases in aircraft engines and during atmospheric reentry.
- Environmental Engineering: Studying air pollution and developing strategies for reducing emissions.
Real-World Examples
- Calculating the Volume of Gas Produced in a Chemical Reaction: When sodium bicarbonate (baking soda) reacts with hydrochloric acid, carbon dioxide gas is produced. Using the ideal gas law with the appropriate value of R, the volume of CO₂ produced at a given temperature and pressure can be calculated.
- Determining the Molar Mass of an Unknown Gas: By measuring the pressure, volume, and temperature of a known mass of an unknown gas, the molar mass can be determined using the ideal gas law. This is a common technique in analytical chemistry.
- Predicting Weather Patterns: Meteorologists use the ideal gas law to model the behavior of air masses and predict weather patterns. Changes in temperature, pressure, and humidity can be related to changes in volume and density, which affect atmospheric stability and wind patterns.
The Van der Waals Equation: Accounting for Non-Ideal Gases
While the ideal gas law is a useful approximation, it does not accurately describe the behavior of gases under all conditions. Real gases deviate from ideal behavior, especially at high pressures and low temperatures, due to intermolecular forces and the finite volume of gas molecules. The Van der Waals equation is a modified version of the ideal gas law that accounts for these deviations:
(P + a(n/V)²) (V - nb) = nRT
Where:
- a is a parameter that accounts for the intermolecular forces between gas molecules.
- b is a parameter that accounts for the volume occupied by the gas molecules.
The Role of R in the Van der Waals Equation
Even in the Van der Waals equation, the value of R remains crucial as it continues to serve as the proportionality constant that relates energy to temperature. The Van der Waals equation is an improvement over the ideal gas law, it incorporates empirical constants (a and b) specific to each gas, allowing for more accurate predictions of gas behavior under non-ideal conditions.
Common Mistakes and How to Avoid Them
When working with the ideal gas law and the value of R, several common mistakes can lead to incorrect results. Being aware of these pitfalls and following best practices can ensure accurate calculations.
1. Incorrect Units
Using the wrong units for pressure, volume, or temperature is a frequent error. Always convert all values to a consistent set of units before using the ideal gas law. For example, if using R = 0.0821 L·atm/mol·K, make sure pressure is in atmospheres, volume is in liters, and temperature is in Kelvin.
How to Avoid:
- Double-check the units of all variables.
- Use conversion factors to convert to the correct units.
- Write out the units in each step of the calculation to ensure consistency.
2. Forgetting to Convert Temperature to Kelvin
Temperature must always be in Kelvin when using the ideal gas law. Failing to convert from Celsius or Fahrenheit to Kelvin is a common mistake.
How to Avoid:
- Always add 273.15 to the Celsius temperature to convert to Kelvin: T(K) = T(°C) + 273.15.
3. Using the Wrong Value of R
There are different values of R depending on the units used for pressure and volume. Using the wrong value of R will lead to incorrect results.
How to Avoid:
- Choose the value of R that matches the units of pressure and volume.
- If necessary, convert pressure and volume to match a known value of R.
4. Assuming All Gases are Ideal
The ideal gas law is an approximation that works well for many gases under certain conditions, but it is not always accurate. Real gases deviate from ideal behavior, especially at high pressures and low temperatures.
How to Avoid:
- Be aware of the limitations of the ideal gas law.
- Consider using the Van der Waals equation or other more accurate equations of state for gases under non-ideal conditions.
5. Incorrectly Applying Stoichiometry
When using the ideal gas law in stoichiometric calculations, make sure to correctly account for the mole ratios of the reactants and products.
How to Avoid:
- Write out the balanced chemical equation for the reaction.
- Use the stoichiometric coefficients to determine the number of moles of each gas involved in the reaction.
The Future of Gas Laws and the Value of R
As scientific understanding advances, new equations of state and models are being developed to better describe the behavior of gases under extreme conditions. These models often incorporate additional parameters to account for complex intermolecular interactions and quantum effects.
Advanced Equations of State
Equations like the Peng-Robinson equation of state and the Redlich-Kwong equation of state offer improved accuracy over the Van der Waals equation, especially for gases at high pressures and densities. These equations are widely used in the petroleum and chemical industries.
Computational Modeling
Computational fluid dynamics (CFD) and molecular dynamics simulations are increasingly used to model the behavior of gases at the molecular level. These simulations can provide detailed insights into the interactions between gas molecules and the effects of temperature and pressure.
Quantum Effects
At very low temperatures, quantum effects become important, and the classical ideal gas law is no longer valid. Quantum statistical mechanics is needed to accurately describe the behavior of gases under these conditions.
Continued Importance of R
Despite these advancements, the value of R remains a fundamental constant in gas laws and related equations. It continues to serve as the bridge between macroscopic and microscopic properties, ensuring that calculations are grounded in basic physical principles. Even in advanced models, R provides a crucial reference point for understanding gas behavior.
Conclusion: The Enduring Legacy of R
The ideal gas constant (R) is more than just a number; it is a cornerstone of chemistry, physics, and engineering. Its value lies in its ability to connect the macroscopic properties of gases to their microscopic behavior, allowing scientists and engineers to make accurate predictions and design efficient systems. From determining the volume of gas produced in a chemical reaction to modeling atmospheric conditions, R plays a vital role in our understanding of the world around us. By understanding its origins, significance, and applications, we can better appreciate the power of this fundamental constant and its enduring legacy in scientific discovery. Properly understanding the value of R in PV=nRT is paramount to understanding many concepts in science.
Latest Posts
Latest Posts
-
Identification Of Unknown Bacteria Lab Report
Nov 28, 2025
-
What Are The Properties Of Ionic
Nov 28, 2025
-
To Calculate Gdp By The Expenditure Method One Must Add
Nov 28, 2025
-
Root Mean Square Speed Of Gas Molecules
Nov 28, 2025
-
Biologists Divide Barriers Of Reproductive Isolation Into 2 Groups
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Value Of R In Pv Nrt . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.