The Symbol For Population Variance Is
penangjazz
Nov 16, 2025 · 10 min read
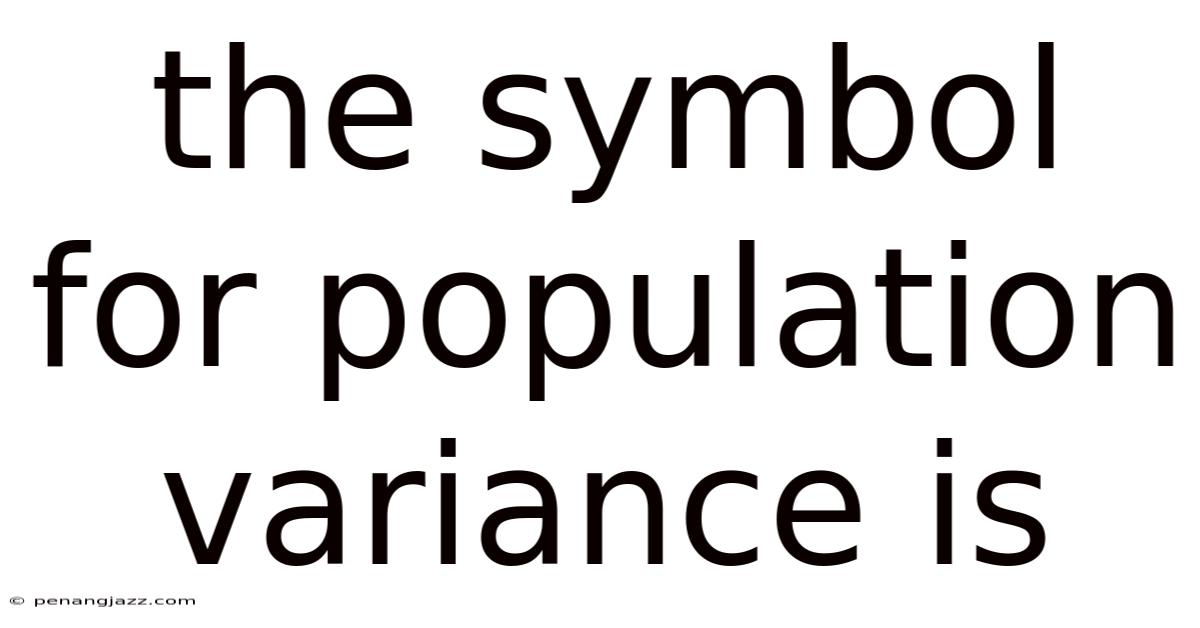
Table of Contents
Population variance, a crucial concept in statistics, measures the spread of data points in a population around the mean. Understanding its symbol and calculation is fundamental for anyone delving into data analysis, research, or decision-making based on statistical insights.
The Symbol for Population Variance: Demystified
The symbol for population variance is σ² (sigma squared). Let's break down what this symbol represents:
- σ (sigma): This is the Greek lowercase letter used to represent the standard deviation of a population. Standard deviation, in essence, is the square root of the variance, providing a measure of data dispersion in the same units as the original data.
- ² (squared): The superscript "2" indicates that we are squaring the standard deviation. Squaring the deviations from the mean results in a positive value, which is essential for calculating variance.
Therefore, σ² succinctly represents the population variance, a core measure of variability within an entire population. It is crucial to differentiate this from sample variance, which uses a different symbol and formula to account for the fact that it's based on a subset of the population.
Why Population Variance Matters
Understanding and calculating population variance is critical for several reasons:
- Data Distribution: Variance provides insight into how spread out the data points are. A high variance indicates that the data is widely dispersed, while a low variance suggests that the data points are clustered closely around the mean.
- Statistical Inference: Population variance is used in various statistical tests and models, such as t-tests, ANOVA, and regression analysis, to make inferences about populations based on sample data.
- Risk Assessment: In fields like finance, variance is used as a measure of risk. A higher variance in investment returns indicates a higher level of risk.
- Quality Control: In manufacturing and other industries, variance is used to monitor the consistency of production processes.
- Decision-Making: Variance helps in making informed decisions by quantifying the uncertainty associated with different options.
Distinguishing Population Variance from Sample Variance
While both population and sample variance measure data dispersion, they differ in their scope and calculation:
| Feature | Population Variance (σ²) | Sample Variance (s²) |
|---|---|---|
| Scope | Measures variability across the entire population. | Measures variability within a subset (sample) of the population. |
| Data Available | Requires data for all members of the population (often impractical). | Uses data from a randomly selected sample. |
| Symbol | σ² | s² |
| Formula | σ² = Σ(xᵢ - μ)² / N, where μ is the population mean and N is the population size. | s² = Σ(xᵢ - x̄)² / (n - 1), where x̄ is the sample mean and n is the sample size. |
| Denominator | Divides by the total number of data points in the population (N). | Divides by (n - 1), which is the sample size minus 1. This is known as Bessel's correction. |
| Bessel's Correction | Not applied | Applied to provide an unbiased estimate of the population variance. |
Why Bessel's Correction (n-1)?
Dividing by 'n' in the sample variance formula would underestimate the population variance. Subtracting 1 from the sample size (n-1) corrects for this bias, especially in smaller samples. This correction is based on the degrees of freedom, which reflect the number of independent pieces of information available to estimate the population variance.
Calculating Population Variance: A Step-by-Step Guide
Here's how to calculate population variance, along with an example:
1. Gather the Data: Collect data for every member of the population you're studying. This is the most challenging part, as obtaining data for an entire population can be difficult or impossible in many real-world scenarios.
2. Calculate the Population Mean (μ): This is the average of all data points in the population. Use the following formula:
μ = Σxᵢ / N
where:
- xᵢ represents each individual data point in the population.
- Σxᵢ is the sum of all data points in the population.
- N is the total number of data points in the population.
3. Calculate the Deviations from the Mean: Subtract the population mean (μ) from each data point (xᵢ) to find the deviation for each value. (xᵢ - μ)
4. Square the Deviations: Square each of the deviations calculated in the previous step. This eliminates negative values and emphasizes larger deviations. (xᵢ - μ)²
5. Sum the Squared Deviations: Add up all the squared deviations. This gives you the total sum of squares. Σ(xᵢ - μ)²
6. Divide by the Population Size (N): Divide the sum of squared deviations by the total number of data points in the population (N). This gives you the population variance (σ²).
σ² = Σ(xᵢ - μ)² / N
Example:
Let's say we have the following data representing the ages of all 5 employees (our population) in a very small company: 25, 30, 35, 40, 45
-
Gather the Data: Ages: 25, 30, 35, 40, 45. N = 5
-
Calculate the Population Mean (μ):
μ = (25 + 30 + 35 + 40 + 45) / 5 = 175 / 5 = 35
-
Calculate the Deviations from the Mean:
- 25 - 35 = -10
- 30 - 35 = -5
- 35 - 35 = 0
- 40 - 35 = 5
- 45 - 35 = 10
-
Square the Deviations:
- (-10)² = 100
- (-5)² = 25
- (0)² = 0
- (5)² = 25
- (10)² = 100
-
Sum the Squared Deviations:
Σ(xᵢ - μ)² = 100 + 25 + 0 + 25 + 100 = 250
-
Divide by the Population Size (N):
σ² = 250 / 5 = 50
Therefore, the population variance (σ²) of the employees' ages is 50. The standard deviation (σ) would be the square root of 50, which is approximately 7.07.
Common Mistakes to Avoid
When working with population variance, be mindful of these common errors:
- Confusing Population and Sample Variance: Always use the correct formula and symbol depending on whether you are dealing with the entire population or just a sample. Remember Bessel's correction for sample variance.
- Incorrectly Calculating the Mean: Double-check your calculations for the mean, as an error here will propagate through the entire variance calculation.
- Forgetting to Square the Deviations: Squaring the deviations is crucial. Skipping this step will result in an incorrect variance value.
- Using Sample Data for Population Variance: If you only have sample data, you cannot directly calculate the population variance. You must use the sample variance formula (with Bessel's correction) to estimate it.
- Misinterpreting Variance: Remember that variance is measured in squared units. For example, if you are measuring heights in inches, the variance will be in inches squared. This can make it difficult to interpret directly, which is why standard deviation (the square root of variance) is often preferred.
Understanding the Implications of High vs. Low Variance
The magnitude of the population variance has significant implications:
High Variance:
- Greater Variability: Data points are widely dispersed around the mean.
- Higher Risk/Uncertainty: In fields like finance, high variance indicates greater volatility and risk.
- Less Predictability: It's harder to make accurate predictions based on the data.
- Potential Outliers: A high variance may indicate the presence of outliers (extreme values) in the dataset.
Low Variance:
- Less Variability: Data points are clustered closely around the mean.
- Lower Risk/Uncertainty: Indicates more stability and predictability.
- Greater Predictability: Easier to make accurate predictions based on the data.
- More Homogeneous Data: The data points are more similar to each other.
Example Scenarios:
- Investment Portfolio: A portfolio with high variance in returns is considered riskier than one with low variance.
- Manufacturing Process: Low variance in product dimensions indicates a consistent and well-controlled process.
- Exam Scores: High variance in exam scores might suggest that some students are struggling while others are excelling.
Advanced Applications of Population Variance
Beyond the basic calculation and interpretation, population variance plays a role in more advanced statistical techniques:
- Hypothesis Testing: Variance is used in tests like ANOVA (Analysis of Variance) to compare the means of multiple groups.
- Confidence Intervals: Population variance (or its estimate from sample data) is used to calculate confidence intervals for population parameters.
- Regression Analysis: Variance is used to assess the goodness of fit of a regression model. The lower the variance of the residuals (the differences between the predicted and actual values), the better the model fits the data.
- Time Series Analysis: Variance is used to analyze the volatility of time series data, such as stock prices or economic indicators.
- Statistical Process Control (SPC): In manufacturing, control charts use variance to monitor process stability and identify potential problems.
Tools for Calculating Population Variance
While the formulas are straightforward, calculating population variance by hand can be tedious, especially with large datasets. Fortunately, several tools can automate this process:
- Spreadsheet Software (e.g., Microsoft Excel, Google Sheets): These programs have built-in functions for calculating population variance (
VAR.Pin Excel,VARPin Google Sheets). You simply enter the data into a column and use the function to calculate the variance. - Statistical Software Packages (e.g., SPSS, R, SAS): These packages offer more advanced statistical capabilities and can handle very large datasets. They also provide options for performing more complex analyses involving variance.
- Online Variance Calculators: Many websites offer free online variance calculators. These are convenient for quick calculations but may not be suitable for large or sensitive datasets.
- Programming Languages (e.g., Python): Libraries like NumPy and SciPy in Python provide functions for calculating variance and other statistical measures. This offers flexibility and control over the calculations.
Example using Python (NumPy):
import numpy as np
data = [25, 30, 35, 40, 45] # Our population data
variance = np.var(data)
print(variance) # Output: 50.0
Addressing Limitations of Population Variance
While a valuable tool, population variance has limitations:
- Sensitivity to Outliers: Outliers can significantly inflate the variance, making it a less reliable measure of dispersion in some cases. Robust measures of dispersion, such as the median absolute deviation (MAD), may be more appropriate when outliers are present.
- Squared Units: As mentioned earlier, variance is measured in squared units, which can be difficult to interpret directly. Standard deviation, which is in the same units as the original data, is often preferred for this reason.
- Requirement for Complete Population Data: Calculating population variance requires data for every member of the population, which is often impractical or impossible to obtain. In such cases, sample variance is used to estimate the population variance.
- Assumes a Single Population: Variance is designed for analyzing a single population. When comparing the variability of multiple populations, other techniques, such as the F-test, may be more appropriate.
Population Variance in Different Fields
The concept of population variance transcends statistical theory and finds practical applications across various disciplines:
- Finance: In finance, variance is a core element of portfolio management, quantifying the risk associated with investments. A higher variance typically equates to greater volatility and, consequently, higher potential risk. Investors use variance to assess the stability and predictability of returns on different assets.
- Manufacturing: Variance plays a crucial role in quality control within manufacturing processes. Monitoring the variance in product dimensions or performance metrics helps manufacturers ensure consistency and identify potential deviations from desired standards.
- Healthcare: In healthcare, population variance can be used to analyze the spread of diseases or health outcomes across a population. This information is vital for public health officials in developing targeted interventions and resource allocation strategies.
- Education: Educators can use variance to assess the distribution of student performance in assessments. High variance might indicate a diverse range of learning levels within a classroom, prompting educators to tailor their teaching methods accordingly.
- Environmental Science: Environmental scientists use variance to analyze the variability of environmental data, such as temperature, rainfall, or pollutant levels. This helps in understanding environmental trends and identifying potential risks.
- Social Sciences: In social sciences, variance can be employed to analyze the diversity of opinions, attitudes, or behaviors within a population. This helps researchers understand social trends and develop targeted interventions.
- Sports Analytics: In sports, variance can be used to analyze player performance metrics, such as points scored, assists, or rebounds. This information helps coaches and analysts assess player consistency and identify areas for improvement.
Conclusion: Mastering the Symbol and Concept of Population Variance
Understanding the symbol for population variance (σ²) and the underlying concept is essential for anyone working with data. By grasping the formula, the difference between population and sample variance, and the implications of high and low variance, you can gain valuable insights into data distribution, risk assessment, and decision-making in various fields. While population variance has limitations, it remains a fundamental tool in statistical analysis and a cornerstone for more advanced techniques. Mastery of this concept empowers you to analyze data effectively and draw meaningful conclusions.
Latest Posts
Latest Posts
-
Six Functions Of The Skeletal System
Nov 16, 2025
-
Equation For A Line In 3d
Nov 16, 2025
-
How To Express Your Answer As An Isotope
Nov 16, 2025
-
Speed Of A Wave In A String
Nov 16, 2025
-
What Are Special Properties Of Water
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about The Symbol For Population Variance Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.