Square Root Of 2 X Square Root Of 2
penangjazz
Nov 07, 2025 · 8 min read
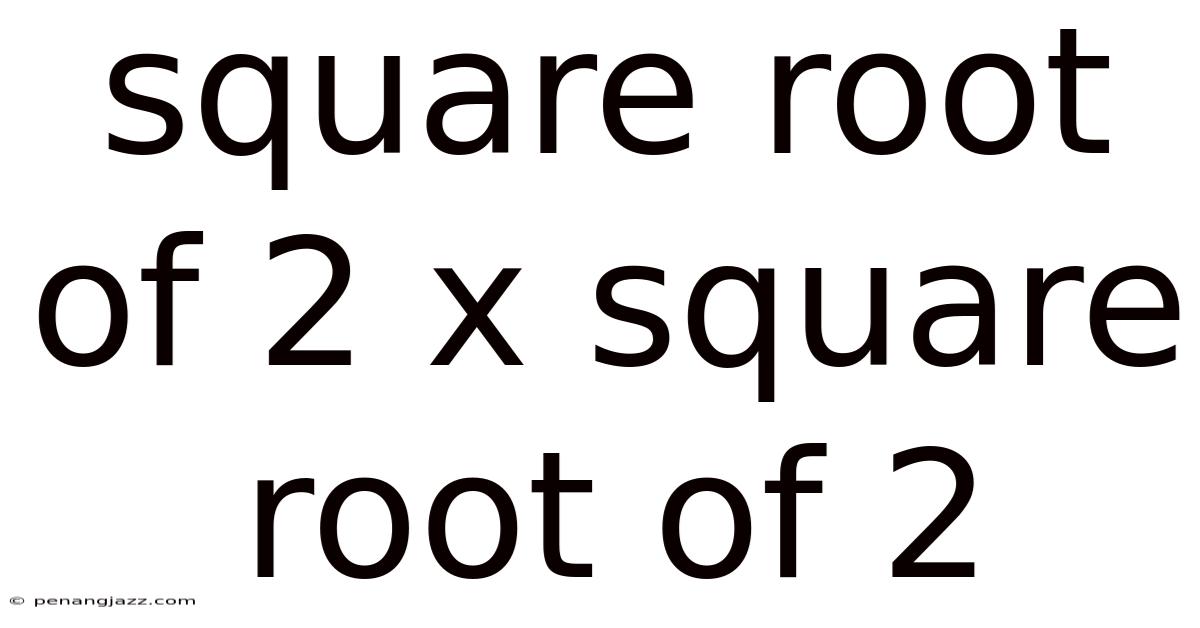
Table of Contents
The square root of 2 multiplied by the square root of 2, often represented as √2 * √2, is a fundamental concept in mathematics, particularly within the realms of algebra and number theory. While the result is seemingly simple – it equals 2 – understanding the underlying principles, implications, and various ways to arrive at this conclusion offers profound insights into mathematical operations and the nature of numbers themselves. This article delves into the concept of √2 * √2, exploring its definition, different methods of calculation, real-world applications, historical context, and frequently asked questions to provide a comprehensive understanding.
Understanding Square Roots
Before diving into the specifics of √2 * √2, it's crucial to understand the basics of square roots.
- Definition: The square root of a number 'x' is a value 'y' that, when multiplied by itself, equals 'x'. In mathematical terms, if y * y = x, then y is the square root of x.
- Symbol: The square root is denoted by the symbol √.
- Principal Square Root: Every positive number has two square roots: a positive (or principal) square root and a negative square root. For example, the square roots of 9 are 3 and -3 because 3 * 3 = 9 and (-3) * (-3) = 9. However, the principal square root is the positive one. When we write √9, we are referring to the principal square root, which is 3.
- Irrational Numbers: Some numbers, like 2, have square roots that cannot be expressed as a simple fraction (a/b, where a and b are integers). These numbers are called irrational numbers. The square root of 2 is approximately 1.41421356..., and its decimal representation goes on infinitely without repeating.
The Square Root of 2 (√2)
The square root of 2 is a particularly significant irrational number. It appears in various mathematical and scientific contexts.
- Value: As mentioned earlier, √2 ≈ 1.41421356...
- Importance: √2 is known as Pythagoras' constant, named after the ancient Greek mathematician Pythagoras. It represents the length of the hypotenuse of a right-angled triangle with both of the other two sides equal to 1. This geometric interpretation gives √2 a prominent role in geometry and trigonometry.
- Proof of Irrationality: The fact that √2 is irrational has been known since ancient times. One of the earliest proofs of its irrationality is attributed to Pythagoras' student Hippasus of Metapontum.
Calculating √2 * √2: Different Approaches
Now, let's explore various ways to calculate √2 * √2 and understand why it equals 2.
1. Direct Multiplication
The most straightforward way to understand why √2 * √2 = 2 is by applying the definition of a square root.
- By definition, the square root of a number 'x' is a value that, when multiplied by itself, gives 'x'.
- Therefore, √2 is a number that, when multiplied by itself, equals 2.
- Hence, √2 * √2 = 2.
This direct application of the definition provides an intuitive understanding of the result.
2. Using the Property √(a) * √(b) = √(a*b)
Another approach involves using the property that the product of the square roots of two numbers is equal to the square root of their product.
- Property: √(a) * √(b) = √(a*b)
- Applying this property to √2 * √2, we get: √2 * √2 = √(2 * 2) = √4
- Since the square root of 4 is 2 (because 2 * 2 = 4), we have: √4 = 2
This method utilizes a fundamental property of square roots to arrive at the same conclusion.
3. Squaring the Square Root
This method involves understanding that squaring a square root essentially cancels out the square root operation.
- (√x)^2 = x
- In our case, we can rewrite √2 * √2 as (√2)^2.
- Applying the above property, we get: (√2)^2 = 2
This method highlights the inverse relationship between squaring and taking the square root.
4. Exponential Notation
Expressing square roots using exponential notation provides another perspective.
- The square root of a number 'x' can be written as x^(1/2).
- Therefore, √2 can be written as 2^(1/2).
- Using this notation, √2 * √2 becomes 2^(1/2) * 2^(1/2).
- Applying the rule of exponents that states a^m * a^n = a^(m+n), we get: 2^(1/2) * 2^(1/2) = 2^(1/2 + 1/2) = 2^1 = 2
This method utilizes the properties of exponents to simplify the expression and arrive at the answer.
Why is √2 * √2 = 2 Important?
The result √2 * √2 = 2 may seem trivial, but it has significant implications in various areas of mathematics and science.
1. Foundation of Mathematical Principles
It serves as a fundamental building block in understanding more complex mathematical concepts.
- Algebra: It is used in simplifying algebraic expressions involving square roots.
- Calculus: It appears in calculus problems involving derivatives and integrals of functions containing square roots.
- Number Theory: It reinforces the properties of irrational numbers and their behavior under mathematical operations.
2. Geometric Significance
As mentioned earlier, √2 represents the length of the hypotenuse of a right-angled triangle with sides of length 1. This geometric interpretation is crucial in trigonometry and geometry.
- Trigonometry: The sine and cosine of 45 degrees (π/4 radians) are related to √2. Specifically, sin(45°) = cos(45°) = 1/√2, which is equivalent to √2/2.
- Geometry: √2 is used in calculating the diagonal of a square with sides of length 1. The diagonal is √2, demonstrating the application of the Pythagorean theorem (a^2 + b^2 = c^2).
3. Practical Applications
Beyond theoretical mathematics, √2 has practical applications in various fields.
- Engineering: Engineers use √2 in structural calculations, especially in designs involving right angles and squares.
- Computer Graphics: In computer graphics, √2 is used in calculating distances and scaling factors, particularly in tasks related to rendering and transformations.
- Physics: √2 appears in various physics formulas, especially those involving energy and wave phenomena.
4. Decimal Approximation and Error Analysis
Understanding that √2 * √2 = 2 is also essential when dealing with decimal approximations of √2. Since √2 is irrational, its decimal representation is non-terminating and non-repeating. When we use a truncated decimal approximation, such as 1.414, multiplying it by itself will not exactly equal 2.
- (1.414) * (1.414) = 1.999396
- The difference between the result and 2 highlights the error introduced by using a decimal approximation.
- In situations requiring high precision, it's important to understand this error and choose an appropriate level of approximation.
Historical Context
The study of √2 dates back to ancient civilizations.
- Pythagoreans: The Pythagoreans, a school of ancient Greek philosophers and mathematicians, were fascinated by numbers and their properties. They initially believed that all numbers could be expressed as ratios of integers (i.e., rational numbers). However, the discovery of √2 challenged this belief.
- Hippasus of Metapontum: As legend has it, Hippasus, a Pythagorean, discovered the irrationality of √2 while trying to calculate the side length of a pentagon. This discovery was unsettling to the Pythagoreans, as it contradicted their fundamental beliefs about the nature of numbers.
- Geometric Proofs: Ancient mathematicians developed geometric proofs to demonstrate the irrationality of √2. These proofs relied on geometric constructions and logical reasoning.
Common Misconceptions
- Misconception: √2 * √2 is approximately equal to 2.
- Clarification: √2 * √2 is exactly equal to 2. The approximation comes into play when we use decimal representations of √2.
- Misconception: √2 * √2 is a complex calculation.
- Clarification: The calculation is straightforward and follows directly from the definition of a square root.
- Misconception: The negative square root of 2 multiplied by itself equals 2.
- Clarification: While (-√2) * (-√2) also equals 2, it is important to distinguish between the principal square root (positive) and the negative square root.
Real-World Examples
To further illustrate the significance of √2 * √2 = 2, let's consider some real-world examples.
1. Construction and Architecture
Suppose you are designing a square garden with sides of length √2 meters. The area of the garden would be:
- Area = side * side = √2 * √2 = 2 square meters
This simple calculation shows how √2 * √2 directly relates to real-world measurements.
2. Navigation and Mapping
In navigation, consider a map where each unit represents a kilometer. If you travel 1 km east and then 1 km north, the straight-line distance from your starting point can be calculated using the Pythagorean theorem. The distance is the hypotenuse of a right-angled triangle with sides of length 1 km.
- Distance = √(1^2 + 1^2) = √2 km
Now, suppose you want to travel this distance back to your starting point and then travel the same distance again in the same direction. The total distance traveled in that direction would be:
- Total Distance = √2 + √2 = 2√2
However, if you think about traveling √2 km two times in the same direction, it is effectively (√2)^2, which is 2.
3. Image Processing
In image processing, images are often represented as arrays of pixels. Consider a simple image processing task where you need to scale an image that has a diagonal length of √2 inches to a size where the diagonal is doubled. The new diagonal length would be:
- New Diagonal Length = 2 * √2
If you then need to calculate the square of this length for some other operation:
- (2 * √2)^2 = 2^2 * (√2)^2 = 4 * 2 = 8
This shows how √2 and its properties are used in image processing calculations.
The Beauty of Simplicity
The equation √2 * √2 = 2 exemplifies the beauty of simplicity in mathematics. Despite its straightforward nature, it unveils fundamental principles and connections across various mathematical and scientific disciplines. From ancient geometric proofs to modern engineering applications, this equation demonstrates the enduring relevance of basic mathematical concepts.
Conclusion
In summary, √2 * √2 = 2 is a fundamental concept with far-reaching implications. Understanding this equation involves grasping the definition of square roots, utilizing properties of square roots, appreciating its geometric significance, and recognizing its practical applications. From its discovery by ancient mathematicians to its use in modern technologies, √2 continues to be a cornerstone of mathematical knowledge. Mastering this concept provides a solid foundation for exploring more advanced topics in mathematics, science, and engineering.
Latest Posts
Latest Posts
-
What Tool Is Used For Measuring Mass
Nov 07, 2025
-
The Body Region Located Beneath The Stomach Is The
Nov 07, 2025
-
Examples Of A Liquid Dissolved In A Liquid
Nov 07, 2025
-
How Do You Find The Empirical Formula Of A Compound
Nov 07, 2025
-
What Is The Product Of Translation
Nov 07, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 X Square Root Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.