Is 7 8 Bigger Than 3 4
penangjazz
Nov 07, 2025 · 8 min read
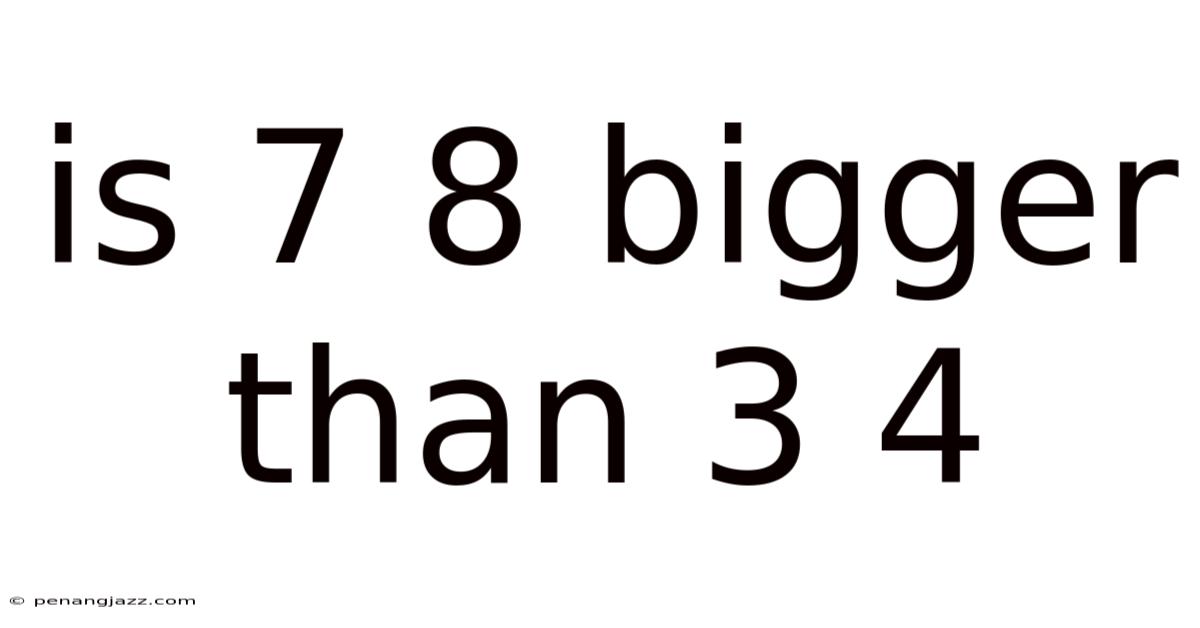
Table of Contents
Comparing fractions might seem tricky at first, but it's a fundamental skill in mathematics with practical applications in everyday life, from cooking and baking to measuring ingredients and understanding proportions. The question of whether 7/8 is bigger than 3/4 is a perfect starting point to explore the world of fractions. Let's break down the concepts, explore different methods, and definitively answer the question, providing you with a solid understanding of fraction comparison.
Understanding Fractions: The Basics
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's written as a/b, where:
- a is the numerator: It represents the number of parts we have.
- b is the denominator: It represents the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) indicates we have one part, and the denominator (2) indicates the whole is divided into two equal parts. This is commonly understood as "one-half."
Methods for Comparing Fractions
Several methods can be used to compare fractions. We will explore four common and effective techniques:
- Finding a Common Denominator
- Converting to Decimals
- Cross-Multiplication
- Visual Representation
Let's examine each method in detail.
1. Finding a Common Denominator
This is one of the most reliable and widely used methods. To compare fractions using a common denominator, we need to:
- Find the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators.
- Convert each fraction so that it has the LCM as its new denominator. To do this, multiply both the numerator and denominator of each fraction by the factor that makes the original denominator equal to the LCM.
- Compare the numerators. Once the fractions have the same denominator, the fraction with the larger numerator is the larger fraction.
Applying the Method to 7/8 and 3/4:
-
Find the LCM of 8 and 4: The multiples of 4 are 4, 8, 12, 16,... The multiples of 8 are 8, 16, 24, 32,... The least common multiple is 8.
-
Convert the fractions:
- 7/8 already has the desired denominator.
- To convert 3/4 to have a denominator of 8, we multiply both the numerator and the denominator by 2: (3 * 2) / (4 * 2) = 6/8
-
Compare the numerators: Now we compare 7/8 and 6/8. Since 7 is greater than 6, 7/8 is greater than 6/8.
Conclusion: 7/8 is bigger than 3/4.
2. Converting to Decimals
Another straightforward method is to convert each fraction to its decimal equivalent. This is done by dividing the numerator by the denominator. Once converted, comparing the decimal values is simple.
Applying the Method to 7/8 and 3/4:
-
Convert 7/8 to a decimal: Divide 7 by 8. The result is 0.875.
-
Convert 3/4 to a decimal: Divide 3 by 4. The result is 0.75.
-
Compare the decimals: Comparing 0.875 and 0.75, we see that 0.875 is greater than 0.75.
Conclusion: 7/8 is bigger than 3/4.
3. Cross-Multiplication
Cross-multiplication is a quick method for comparing two fractions. To use this method:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the results. If the first product is greater than the second product, then the first fraction is greater than the second fraction. If the second product is greater, then the second fraction is greater. If the products are equal, the fractions are equal.
Applying the Method to 7/8 and 3/4:
-
Multiply 7 (numerator of the first fraction) by 4 (denominator of the second fraction): 7 * 4 = 28
-
Multiply 3 (numerator of the second fraction) by 8 (denominator of the first fraction): 3 * 8 = 24
-
Compare the results: 28 is greater than 24.
Conclusion: 7/8 is bigger than 3/4.
4. Visual Representation
Visualizing fractions can make the comparison intuitive, especially for those who are visual learners. We can use diagrams, such as pie charts or rectangles, to represent the fractions and then compare the shaded areas.
Applying the Method to 7/8 and 3/4:
-
Draw two identical rectangles.
-
Divide the first rectangle into 8 equal parts and shade 7 of those parts to represent 7/8.
-
Divide the second rectangle into 4 equal parts and shade 3 of those parts to represent 3/4.
-
Visually compare the shaded areas. It’s clear that the shaded area representing 7/8 is larger than the shaded area representing 3/4.
Conclusion: 7/8 is bigger than 3/4.
Real-World Applications of Comparing Fractions
Understanding how to compare fractions is not just an academic exercise; it has numerous practical applications in everyday life:
- Cooking and Baking: Recipes often require adjusting ingredient quantities. Knowing how to compare fractions allows you to accurately increase or decrease recipes. For example, if a recipe calls for 3/4 cup of flour and you want to double the recipe, you need to know that 3/4 + 3/4 = 6/4, which simplifies to 1 1/2 cups.
- Measuring: Whether you're measuring wood for a carpentry project or fabric for sewing, comparing fractions is essential. Understanding that 5/8 of an inch is smaller than 3/4 of an inch helps you make precise cuts and avoid errors.
- Time Management: Dividing tasks and allocating time often involves fractions. If you need to allocate 1/3 of your day to work and 1/4 to exercise, knowing which fraction represents more time helps you plan your schedule effectively.
- Financial Planning: When dealing with investments or budgeting, fractions are commonly used to represent portions of your income or expenses. Comparing these fractions helps you understand where your money is going and make informed financial decisions.
- Construction and Engineering: Precise measurements are critical in these fields. Engineers and construction workers frequently use fractions to calculate dimensions, angles, and material quantities. Accurate comparison of fractions ensures structural integrity and safety.
Common Mistakes to Avoid
While comparing fractions is relatively straightforward, there are common mistakes that can lead to incorrect conclusions:
- Assuming Larger Denominator Means Larger Fraction: It's a common misconception to think that a fraction with a larger denominator is always smaller. This is only true when comparing fractions with the same numerator. For example, 1/100 is indeed smaller than 1/2. However, when numerators differ, this assumption is incorrect (e.g., 7/8 > 3/4).
- Incorrectly Finding the Least Common Multiple (LCM): Using the wrong LCM can lead to incorrect conversions and comparisons. Always double-check your LCM calculations.
- Arithmetic Errors: Simple addition, subtraction, multiplication, or division errors during the conversion or comparison process can lead to incorrect results. Take your time and verify your calculations.
- Forgetting to Simplify: Sometimes, simplifying fractions before comparing them can make the process easier. Forgetting to simplify can lead to unnecessary complexity.
- Misinterpreting Visual Representations: When using visual methods, ensure that the diagrams are accurately drawn and divided into equal parts. Inaccurate diagrams can lead to incorrect visual comparisons.
Advanced Fraction Concepts
Once you're comfortable with basic fraction comparison, you can explore more advanced concepts:
- Mixed Numbers: A mixed number is a combination of a whole number and a fraction (e.g., 2 1/2). To compare mixed numbers, first compare the whole numbers. If the whole numbers are equal, then compare the fractional parts.
- Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/2). Improper fractions can be converted to mixed numbers, which can then be compared.
- Complex Fractions: A complex fraction is a fraction where the numerator, the denominator, or both contain fractions (e.g., (1/2) / (3/4)). To simplify complex fractions, multiply the numerator by the reciprocal of the denominator.
- Fractions in Algebra: Fractions are extensively used in algebra to represent variables, coefficients, and constants. Understanding how to manipulate and compare algebraic fractions is essential for solving equations and simplifying expressions.
The Importance of a Strong Foundation in Fractions
Mastering fractions is crucial for building a solid mathematical foundation. Fractions are not just abstract concepts; they are fundamental tools used in various fields, including:
- Mathematics: Fractions are foundational to algebra, geometry, calculus, and other advanced mathematical disciplines. A strong understanding of fractions is essential for success in these areas.
- Science: Fractions are used in physics, chemistry, biology, and other scientific fields to represent ratios, proportions, and measurements.
- Engineering: Engineers rely heavily on fractions to design structures, calculate forces, and analyze data.
- Finance: Financial analysts use fractions to calculate interest rates, returns on investment, and other financial metrics.
- Technology: Programmers and computer scientists use fractions to represent probabilities, ratios, and proportions in algorithms and data structures.
Practice Problems
To solidify your understanding, try solving these practice problems:
- Compare 2/3 and 5/8.
- Compare 4/5 and 7/9.
- Compare 11/12 and 13/15.
- Compare 9/10 and 5/6.
- Compare 1/2 and 4/9.
Answers:
- 2/3 > 5/8
- 7/9 > 4/5
- 11/12 > 13/15
- 9/10 > 5/6
- 1/2 > 4/9
Final Thoughts
Comparing fractions is a fundamental mathematical skill with wide-ranging applications. By understanding the basic principles and practicing different methods, you can confidently compare fractions and apply this knowledge in various real-world scenarios. Whether you're cooking, measuring, or solving complex mathematical problems, a solid grasp of fractions is an invaluable asset. And to definitively answer the initial question: yes, 7/8 is indeed bigger than 3/4. Continue practicing and exploring advanced concepts to deepen your understanding and appreciation of fractions.
Latest Posts
Latest Posts
-
Does Zeff Increase Across A Period
Nov 07, 2025
-
What Is Another Name For Light Independent Reactions
Nov 07, 2025
-
How Many Valence Electrons Does S Have
Nov 07, 2025
-
Difference Between Accounting Profit And Economic Profit
Nov 07, 2025
-
How Many Atp Does Glycolysis Produce
Nov 07, 2025
Related Post
Thank you for visiting our website which covers about Is 7 8 Bigger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.