Is 5 8 Greater Than 3 4
penangjazz
Nov 19, 2025 · 8 min read
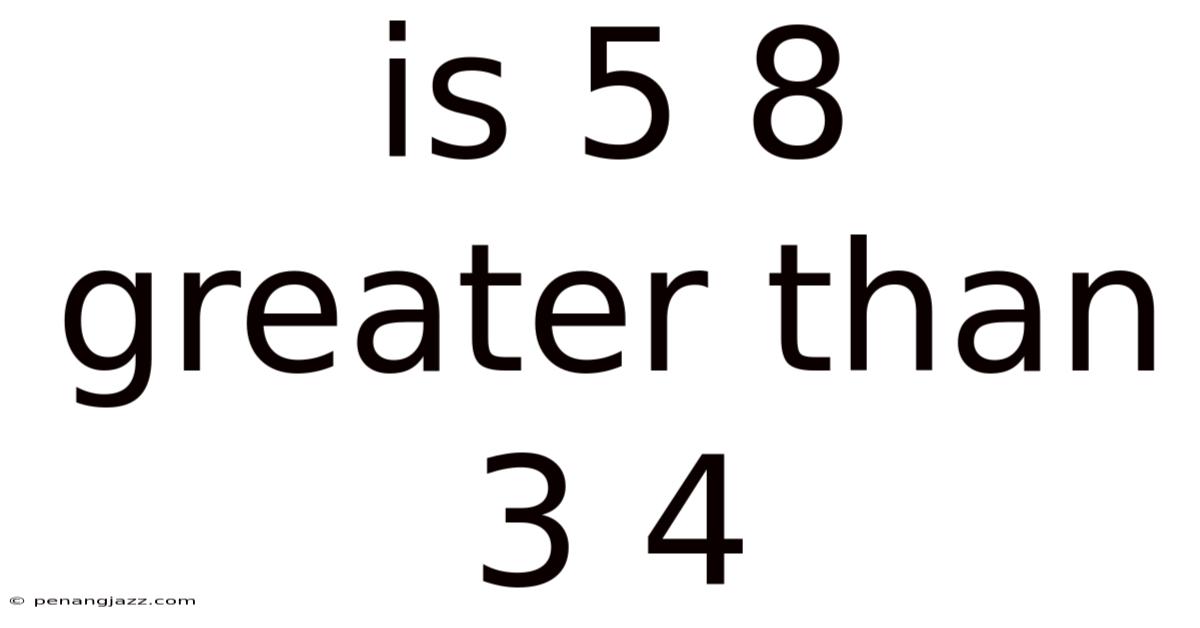
Table of Contents
Navigating the world of fractions can sometimes feel like trying to find your way through a maze. Questions like "Is 5/8 greater than 3/4?" might seem simple on the surface, but they require a solid understanding of fractional values and comparison techniques. This article aims to provide a comprehensive explanation to help you confidently determine whether 5/8 is indeed greater than 3/4, exploring various methods and clarifying the underlying principles.
Understanding Fractions: A Quick Review
Before diving into the comparison of 5/8 and 3/4, it's essential to recap the basics of fractions. A fraction represents a part of a whole, expressed as a ratio between two numbers: the numerator (the top number) and the denominator (the bottom number).
- Numerator: Indicates how many parts of the whole are being considered.
- Denominator: Indicates the total number of equal parts into which the whole is divided.
For instance, in the fraction 5/8:
- 5 is the numerator, showing we have 5 parts.
- 8 is the denominator, indicating the whole is divided into 8 equal parts.
The Challenge: Comparing 5/8 and 3/4
At first glance, it might be challenging to directly compare 5/8 and 3/4. The fractions have different denominators, making a direct comparison of their numerators misleading. To accurately determine which fraction is larger, we need a common ground, which can be achieved through several methods.
Method 1: Finding a Common Denominator
One of the most reliable ways to compare fractions is to find a common denominator. This involves converting both fractions into equivalent fractions with the same denominator. Once the denominators are the same, you can easily compare the numerators to determine which fraction represents a larger portion of the whole.
Steps to Find a Common Denominator:
- Identify the Denominators:
- In our case, the denominators are 8 (from 5/8) and 4 (from 3/4).
- Find the Least Common Multiple (LCM):
- The LCM is the smallest number that is a multiple of both denominators.
- Multiples of 4: 4, 8, 12, 16, ...
- Multiples of 8: 8, 16, 24, 32, ...
- The LCM of 4 and 8 is 8.
- Convert Fractions to Equivalent Fractions with the Common Denominator:
- For 5/8: Since the denominator is already 8, no conversion is needed. The fraction remains 5/8.
- For 3/4: To convert 3/4 to an equivalent fraction with a denominator of 8, we need to multiply both the numerator and the denominator by the same number so that the denominator becomes 8.
- What number multiplied by 4 equals 8? The answer is 2.
- Multiply both the numerator and denominator of 3/4 by 2:
- (3 * 2) / (4 * 2) = 6/8
- Compare the New Fractions:
- Now we have two fractions with the same denominator: 5/8 and 6/8.
- Compare the numerators: 5 and 6.
- Since 6 is greater than 5, 6/8 is greater than 5/8.
Conclusion: Since 6/8 is greater than 5/8, and 6/8 is equivalent to 3/4, we can conclude that 3/4 is greater than 5/8.
Method 2: Cross-Multiplication
Cross-multiplication is a quick and efficient method to compare two fractions without explicitly finding a common denominator. This method involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results.
Steps for Cross-Multiplication:
- Write the Fractions:
- 5/8 and 3/4
- Cross-Multiply:
- Multiply the numerator of the first fraction (5) by the denominator of the second fraction (4):
- 5 * 4 = 20
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (8):
- 3 * 8 = 24
- Multiply the numerator of the first fraction (5) by the denominator of the second fraction (4):
- Compare the Results:
- We have two results: 20 and 24.
- Compare the results: 20 < 24.
- Determine Which Fraction is Larger:
- If the result of the first cross-multiplication (5 * 4) is less than the result of the second cross-multiplication (3 * 8), then the first fraction (5/8) is less than the second fraction (3/4).
Conclusion: Since 20 is less than 24, we conclude that 5/8 is less than 3/4.
Method 3: Converting to Decimals
Another way to compare fractions is by converting them into decimal form. Decimals provide a standardized way to represent fractional values, making comparisons straightforward.
Steps to Convert to Decimals:
- Convert 5/8 to a Decimal:
- Divide the numerator (5) by the denominator (8):
- 5 ÷ 8 = 0.625
- Divide the numerator (5) by the denominator (8):
- Convert 3/4 to a Decimal:
- Divide the numerator (3) by the denominator (4):
- 3 ÷ 4 = 0.75
- Divide the numerator (3) by the denominator (4):
- Compare the Decimals:
- Compare 0.625 and 0.75.
-
- 625 < 0.75
Conclusion: Since 0.625 is less than 0.75, we conclude that 5/8 is less than 3/4.
Method 4: Visual Representation
Visual representations can provide an intuitive understanding of fraction comparison. By illustrating the fractions using diagrams, you can visually determine which fraction represents a larger portion of the whole.
Steps for Visual Representation:
- Draw Two Identical Rectangles:
- Representing the "whole" for both fractions.
- Divide the First Rectangle into 8 Equal Parts:
- To represent the denominator of 5/8.
- Shade 5 of these parts to represent the fraction 5/8.
- Divide the Second Rectangle into 4 Equal Parts:
- To represent the denominator of 3/4.
- Shade 3 of these parts to represent the fraction 3/4.
- Compare the Shaded Areas:
- Visually compare the amount of shading in each rectangle.
- You will notice that the shaded area in the rectangle representing 3/4 is larger than the shaded area in the rectangle representing 5/8.
Conclusion: The visual representation confirms that 3/4 is greater than 5/8.
Real-World Examples
Understanding the comparison of fractions is not just an academic exercise; it has practical applications in everyday life. Here are a few examples:
- Cooking:
- Imagine you are following a recipe that requires you to add ingredients in fractional amounts. For instance, the recipe might call for 5/8 cup of flour and 3/4 cup of sugar. Knowing which fraction is greater helps you measure the ingredients accurately, ensuring the recipe turns out correctly.
- Construction:
- In construction, measurements often involve fractions. If you are cutting a piece of wood and need to determine whether a 5/8-inch nail or a 3/4-inch nail is longer, understanding fraction comparison is essential for selecting the right materials.
- Finance:
- Comparing fractions can be useful in understanding financial data. For example, if one investment yields 5/8 of a return and another yields 3/4, comparing these fractions helps you determine which investment is more profitable.
- Time Management:
- If you spend 5/8 of an hour on one task and 3/4 of an hour on another, knowing which fraction is greater helps you manage your time efficiently and allocate the appropriate amount of time to each task.
Common Mistakes to Avoid
When comparing fractions, it's essential to avoid common pitfalls that can lead to incorrect conclusions. Here are a few mistakes to watch out for:
- Directly Comparing Numerators Without a Common Denominator:
- One of the most common mistakes is to compare the numerators of fractions without ensuring they have a common denominator. For example, incorrectly assuming that 5/8 is greater than 3/4 simply because 5 is greater than 3.
- Incorrectly Finding the Least Common Multiple (LCM):
- If you choose an incorrect common multiple, you may end up with larger numbers, making the comparison process more complex. Always ensure you are using the least common multiple.
- Miscalculating Equivalent Fractions:
- When converting fractions to equivalent fractions, ensure you multiply both the numerator and the denominator by the same number. Failing to do so will result in an incorrect equivalent fraction.
- Errors in Cross-Multiplication:
- Double-check your multiplication to avoid errors that can lead to an incorrect comparison.
- Misinterpreting Decimal Values:
- Ensure you correctly interpret the decimal values when comparing fractions. Sometimes, it's easy to make a mistake if you don't pay close attention to the decimal places.
Practice Questions
To reinforce your understanding of comparing fractions, try solving these practice questions:
- Which is greater: 2/3 or 5/9?
- Compare 7/10 and 4/5.
- Is 1/4 greater than or less than 2/8?
- Arrange the following fractions in ascending order: 1/2, 3/8, 2/5.
Answers:
- 2/3 is greater than 5/9. (2/3 = 6/9, and 6/9 > 5/9)
- 4/5 is greater than 7/10. (4/5 = 8/10, and 8/10 > 7/10)
- 1/4 is equal to 2/8. (1/4 = 2/8)
- 3/8, 2/5, 1/2 (Converting to a common denominator of 40: 15/40, 16/40, 20/40)
Conclusion: 3/4 is Greater than 5/8
Through various methods—finding a common denominator, cross-multiplication, converting to decimals, and visual representation—we have consistently demonstrated that 3/4 is greater than 5/8.
Understanding how to compare fractions is a fundamental skill with wide-ranging applications. Whether you're measuring ingredients in the kitchen, managing finances, or working on a construction project, the ability to confidently compare fractions is invaluable. By mastering these techniques and avoiding common mistakes, you can tackle fraction-related challenges with ease and precision.
Latest Posts
Latest Posts
-
Phillips Curve In The Long Run
Nov 19, 2025
-
What Is A Product For Science
Nov 19, 2025
-
Is Tap Water Homogeneous Or Heterogeneous
Nov 19, 2025
-
Are Cells The Smallest Unit Of Life
Nov 19, 2025
-
How Many Bonds Does Nitrogen Have
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about Is 5 8 Greater Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.