Is 1 3 Greater Than 2 5
penangjazz
Nov 23, 2025 · 7 min read
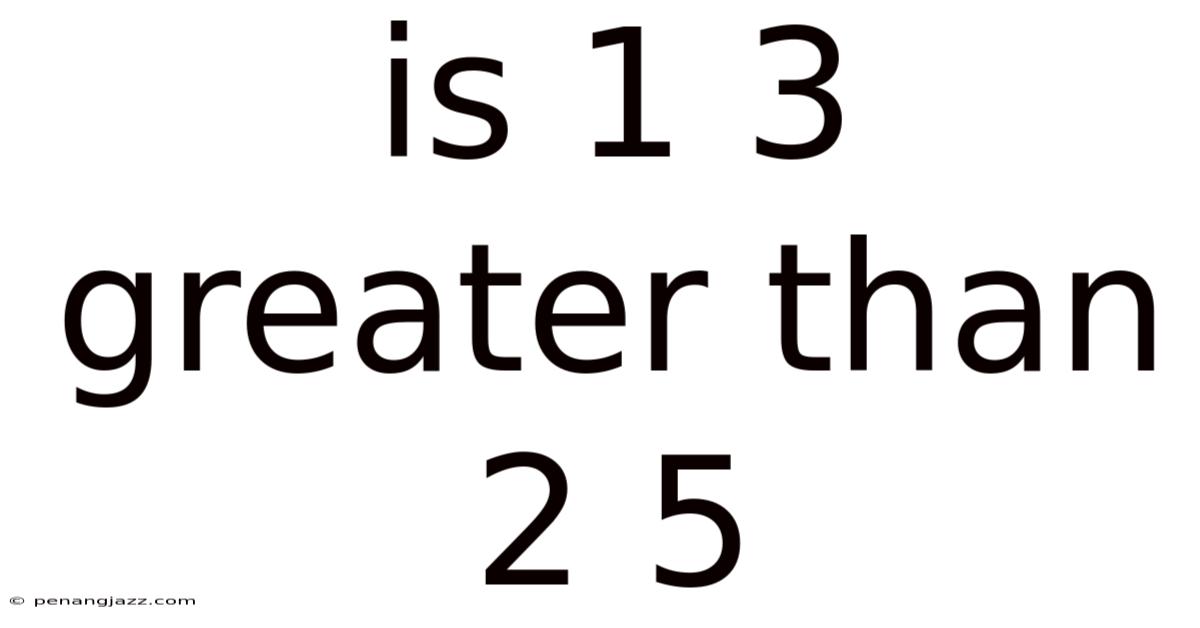
Table of Contents
Comparing fractions might seem tricky at first, but understanding the underlying principles makes it surprisingly straightforward. Whether 1/3 is greater than 2/5 is a common question that can be answered through various methods, all rooted in basic mathematical concepts. This article will explore these methods in detail, ensuring you grasp not only the answer but also the ‘why’ behind it.
Understanding Fractions
Before diving into the comparison, it's essential to understand what fractions represent. A fraction is a way of representing a part of a whole. It consists of two numbers: the numerator (the number on top) and the denominator (the number below).
- Numerator: Indicates how many parts of the whole you have.
- Denominator: Indicates the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) tells us we have one part, and the denominator (3) tells us that the whole is divided into three equal parts. Similarly, in 2/5, we have two parts out of a total of five equal parts.
Methods to Compare Fractions
Several methods can be used to determine whether 1/3 is greater than 2/5. These include:
- Finding a Common Denominator
- Converting to Decimals
- Cross-Multiplication
- Visual Comparison
1. Finding a Common Denominator
The most common method to compare fractions is to find a common denominator. This involves converting the fractions to equivalent fractions with the same denominator. Once the denominators are the same, you can easily compare the numerators to determine which fraction is larger.
Steps:
-
Find the Least Common Multiple (LCM) of the Denominators:
- The denominators are 3 and 5.
- The multiples of 3 are: 3, 6, 9, 12, 15, 18, ...
- The multiples of 5 are: 5, 10, 15, 20, 25, ...
- The least common multiple of 3 and 5 is 15.
-
Convert Each Fraction to an Equivalent Fraction with the Common Denominator:
-
For 1/3:
- To get the denominator 15, we multiply 3 by 5.
- Therefore, we also multiply the numerator 1 by 5.
- So, 1/3 = (1 * 5) / (3 * 5) = 5/15
-
For 2/5:
- To get the denominator 15, we multiply 5 by 3.
- Therefore, we also multiply the numerator 2 by 3.
- So, 2/5 = (2 * 3) / (5 * 3) = 6/15
-
-
Compare the Numerators:
- Now we have 5/15 and 6/15.
- Since 5 is less than 6, 5/15 < 6/15.
Conclusion: 1/3 is less than 2/5.
2. Converting to Decimals
Another straightforward method is to convert each fraction to its decimal equivalent. Decimals are easier to compare because they are based on the base-10 number system, which we use daily.
Steps:
-
Convert 1/3 to a Decimal:
- Divide 1 by 3.
- 1 ÷ 3 = 0.333... (repeating decimal)
-
Convert 2/5 to a Decimal:
- Divide 2 by 5.
- 2 ÷ 5 = 0.4
-
Compare the Decimals:
- We have 0.333... and 0.4.
- Since 0.333... is less than 0.4, 1/3 < 2/5.
Conclusion: 1/3 is less than 2/5.
3. Cross-Multiplication
Cross-multiplication is a quick algebraic method to compare two fractions. It involves multiplying the numerator of the first fraction by the denominator of the second fraction and vice versa.
Steps:
-
Cross-Multiply:
- Multiply the numerator of 1/3 (which is 1) by the denominator of 2/5 (which is 5): 1 * 5 = 5
- Multiply the numerator of 2/5 (which is 2) by the denominator of 1/3 (which is 3): 2 * 3 = 6
-
Compare the Results:
- We have 5 and 6.
- Since 5 is less than 6, 1/3 < 2/5.
Conclusion: 1/3 is less than 2/5.
4. Visual Comparison
Sometimes, visualizing fractions can make the comparison more intuitive. This method involves drawing diagrams to represent the fractions and then visually comparing the shaded areas.
Steps:
-
Draw Two Identical Rectangles:
- These rectangles represent the whole.
-
Divide the First Rectangle into Three Equal Parts and Shade One Part:
- This represents 1/3.
-
Divide the Second Rectangle into Five Equal Parts and Shade Two Parts:
- This represents 2/5.
-
Compare the Shaded Areas:
- Visually, the shaded area representing 2/5 is larger than the shaded area representing 1/3.
Conclusion: 1/3 is less than 2/5.
Real-World Examples
Understanding the comparison of fractions is not just a theoretical exercise. It has practical applications in everyday life.
-
Cooking:
- Imagine you are following a recipe that calls for ingredients in fractional amounts. For example, one recipe requires 1/3 cup of sugar, and another requires 2/5 cup. Knowing how to compare these fractions helps you understand which recipe uses more sugar.
-
Measuring:
- When measuring ingredients or distances, you often encounter fractions. If you need to cut a piece of fabric that is either 1/3 of a yard or 2/5 of a yard, comparing these fractions will help you determine which length is greater.
-
Time Management:
- Suppose you spend 1/3 of your day working and 2/5 of your day sleeping. Comparing these fractions can help you determine whether you spend more time working or sleeping.
-
Financial Planning:
- When budgeting, you might allocate fractions of your income to different categories. If you allocate 1/3 of your income to housing and 2/5 to other expenses, knowing how to compare fractions helps you understand where most of your money is going.
Common Mistakes
When comparing fractions, several common mistakes can lead to incorrect conclusions. Being aware of these mistakes can help you avoid them.
-
Incorrectly Finding the Common Denominator:
- One common mistake is choosing any common multiple instead of the least common multiple. While any common multiple will work, using the LCM simplifies the process and avoids dealing with larger numbers.
-
Comparing Numerators Without a Common Denominator:
- It is incorrect to compare the numerators of fractions directly unless they have the same denominator. For example, you cannot say that 2/5 is greater than 1/3 simply because 2 is greater than 1.
-
Miscalculating Decimal Equivalents:
- When converting fractions to decimals, ensure you perform the division correctly. Rounding errors or incorrect division can lead to wrong comparisons.
-
Relying Solely on Visual Estimation:
- While visual comparison can be helpful, it is not always accurate, especially with fractions that are close in value. It is better to use a more precise method like finding a common denominator or converting to decimals.
Advanced Concepts
For a deeper understanding of fractions, consider exploring these advanced concepts:
-
Improper Fractions and Mixed Numbers:
- An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 5/3). A mixed number consists of a whole number and a fraction (e.g., 1 2/3). Understanding how to convert between improper fractions and mixed numbers is crucial for advanced fraction operations.
-
Operations with Fractions:
- Beyond comparing fractions, it’s essential to understand how to add, subtract, multiply, and divide them. These operations build upon the basic principles of fraction comparison.
-
Fractions in Algebra:
- In algebra, fractions are often used in equations and expressions. Understanding how to manipulate algebraic fractions is essential for solving more complex problems.
FAQs
-
Why do we need a common denominator to compare fractions?
- A common denominator allows us to compare fractions because it expresses them in terms of the same "unit" size. When the denominators are the same, the numerators directly reflect the relative sizes of the fractions.
-
Can I use any common multiple as a common denominator?
- Yes, you can use any common multiple, but using the least common multiple (LCM) makes the calculations simpler.
-
Is cross-multiplication always accurate?
- Yes, cross-multiplication is an accurate method for comparing fractions, as long as you perform the multiplication correctly.
-
What if I have more than two fractions to compare?
- For more than two fractions, find the common denominator for all the fractions, and then compare the numerators.
-
How do I compare negative fractions?
- When comparing negative fractions, remember that the fraction with the smaller absolute value is actually larger. For example, -1/3 is greater than -2/5 because 1/3 is smaller than 2/5.
Conclusion
In summary, comparing fractions is a fundamental skill with wide-ranging applications. Whether 1/3 is greater than 2/5 can be easily determined through methods like finding a common denominator, converting to decimals, cross-multiplication, or visual comparison. All these methods lead to the same conclusion: 1/3 is less than 2/5. Understanding these methods not only answers the question but also equips you with the tools to tackle more complex mathematical problems. From cooking to financial planning, the ability to compare fractions accurately is a valuable asset in everyday life.
Latest Posts
Latest Posts
-
Where Does Cellular Respiration Take Place In Eukaryotic Cells
Nov 23, 2025
-
2 Heat Transfer Through The Collision Of Molecules Direct Contact
Nov 23, 2025
-
How Many Rows Are In The Periodic Table
Nov 23, 2025
-
Meaning Of Demand Schedule In Economics
Nov 23, 2025
-
How To Find The Range Of An Inverse Function
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about Is 1 3 Greater Than 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.