Equation For Decay Of Carbon 14
penangjazz
Nov 16, 2025 · 13 min read
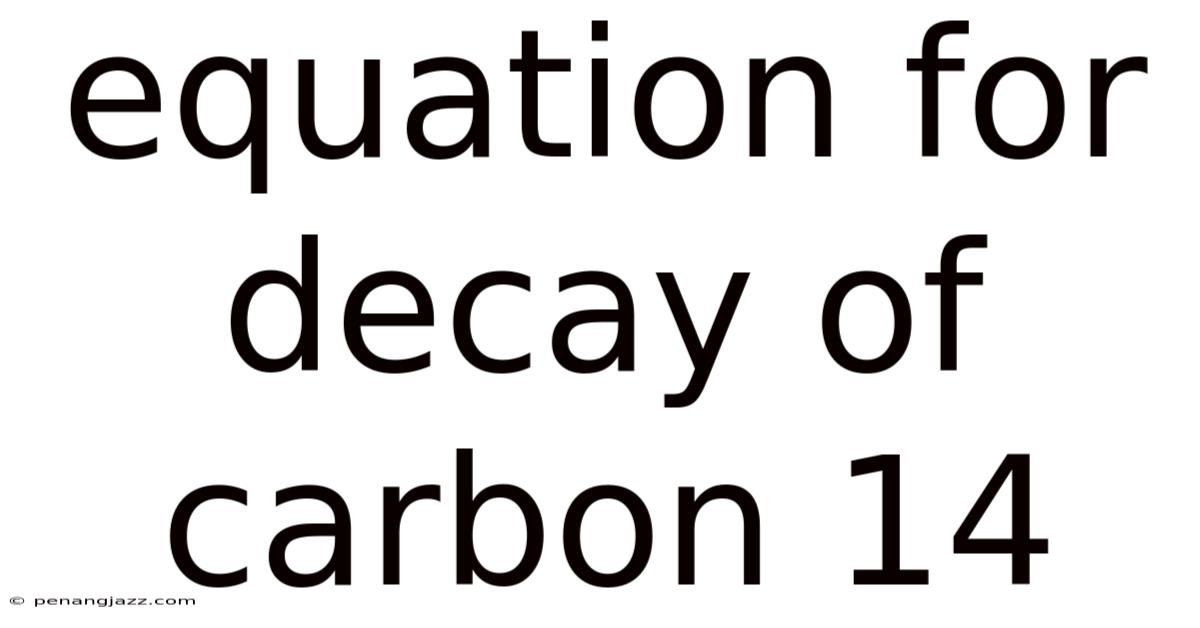
Table of Contents
Radioactive decay, a process governed by the principles of quantum mechanics, allows unstable atomic nuclei to lose energy and mass until they reach a stable state. One of the most famous examples of radioactive decay is that of Carbon-14, a process crucial for radiocarbon dating in various fields, including archaeology and geology. The equation governing the decay of Carbon-14 is a testament to the predictability and mathematical elegance of radioactive decay.
Understanding Carbon-14
Carbon-14 ((^{14}C)) is a radioactive isotope of carbon. Unlike the stable and abundant Carbon-12 ((^{12}C)), Carbon-14 has two extra neutrons in its nucleus. It's continuously formed in the upper atmosphere when neutrons produced by cosmic rays collide with nitrogen atoms. This process replaces a proton in nitrogen with a neutron, transforming it into Carbon-14:
[ n + ^{14}N \rightarrow ^{14}C + p ]
where (n) is a neutron and (p) is a proton.
Carbon-14 is chemically identical to Carbon-12 and, as a result, participates in the same biological and environmental processes. It combines with oxygen to form carbon dioxide, which plants absorb during photosynthesis. Animals then ingest Carbon-14 by eating plants or other animals. This incorporation ensures that all living organisms maintain a consistent ratio of (^{14}C) to (^{12}C) that is in equilibrium with the atmosphere.
However, once an organism dies, it ceases to replenish its carbon content. The Carbon-14 present at the time of death begins to decay, while the amount of Carbon-12 remains constant. This decay follows a well-defined exponential pattern, described by a specific equation.
The Decay Process
Carbon-14 decays into Nitrogen-14 ((^{14}N)) through a process known as beta decay. In beta decay, a neutron in the Carbon-14 nucleus transforms into a proton, emitting an electron (beta particle) and an antineutrino:
[ ^{14}C \rightarrow ^{14}N + e^- + \bar{\nu}_e ]
Here, (e^-) represents the beta particle (electron), and (\bar{\nu}_e) is the antineutrino. This decay process changes the atomic composition of the nucleus, reducing the amount of Carbon-14 over time.
The Decay Equation
The decay of Carbon-14 is governed by the law of radioactive decay, which is a statistical process. It states that the rate of decay is proportional to the number of radioactive atoms present. The differential equation that describes this process is:
[ \frac{dN}{dt} = -\lambda N ]
where:
- (N) is the number of Carbon-14 atoms at time (t),
- (\frac{dN}{dt}) is the rate of change of the number of Carbon-14 atoms with respect to time,
- (\lambda) is the decay constant, which is specific to each radioactive isotope.
The negative sign indicates that the number of Carbon-14 atoms decreases over time. This differential equation can be solved using calculus to obtain the equation for the number of Carbon-14 atoms as a function of time:
[ N(t) = N_0 e^{-\lambda t} ]
where:
- (N(t)) is the number of Carbon-14 atoms at time (t),
- (N_0) is the initial number of Carbon-14 atoms at time (t = 0),
- (e) is the base of the natural logarithm ((\approx 2.71828)),
- (t) is the time elapsed since the organism died.
Half-Life and Decay Constant
A critical parameter in radioactive decay is the half-life ((T_{1/2})), which is the time required for half of the radioactive atoms in a sample to decay. The half-life of Carbon-14 is approximately 5,730 years. The decay constant (\lambda) is related to the half-life by the following equation:
[ T_{1/2} = \frac{\ln(2)}{\lambda} ]
where (\ln(2)) is the natural logarithm of 2 ((\approx 0.693)).
From this, the decay constant (\lambda) can be calculated as:
[ \lambda = \frac{\ln(2)}{T_{1/2}} ]
For Carbon-14, the decay constant is:
[ \lambda = \frac{0.693}{5730 \text{ years}} \approx 1.21 \times 10^{-4} \text{ years}^{-1} ]
Radiocarbon Dating
Radiocarbon dating, also known as carbon-14 dating, is a method for determining the age of a sample containing organic material by using the properties of Carbon-14. The principle behind this dating technique is straightforward: when an organism is alive, it continuously exchanges carbon with its environment, maintaining a stable ratio of (^{14}C) to (^{12}C). Once the organism dies, this exchange stops, and the (^{14}C) begins to decay.
By measuring the remaining amount of (^{14}C) in the sample and comparing it to the initial amount found in living organisms, the age of the sample can be determined. The standard reference point for the initial (^{14}C/^{12}C) ratio is that of living organisms in equilibrium with the atmosphere.
Methodology of Radiocarbon Dating
-
Sample Collection: The process begins with the careful collection of a sample from the organic material of interest. This could include wood, bone, charcoal, or other carbon-containing substances.
-
Sample Preparation: The sample is then pretreated to remove any contaminants that might affect the accuracy of the dating. This pretreatment may involve physical and chemical cleaning processes to isolate the pure carbon.
-
Carbon Isolation: After pretreatment, the carbon in the sample is converted into a suitable form for measurement. This usually involves combustion to convert the carbon into carbon dioxide ((CO_2)). The (CO_2) gas is then purified and converted into graphite or benzene.
-
Measurement of (^{14}C) Content: The amount of (^{14}C) in the sample is measured using one of two primary methods:
- Radiometric Dating (Beta Counting): This traditional method involves counting the number of beta particles emitted by the decaying (^{14}C) atoms in the sample over a specific period. The rate of beta emission is proportional to the amount of (^{14}C) present.
- Accelerator Mass Spectrometry (AMS): AMS is a more modern and sensitive technique that directly counts the number of (^{14}C) atoms in the sample. AMS requires a much smaller sample size and provides more precise results than radiometric dating.
-
Age Calculation: Once the (^{14}C) content of the sample is measured, the age of the sample can be calculated using the decay equation:
[ t = \frac{\ln(N_0/N(t))}{\lambda} ]
where:
- (t) is the age of the sample,
- (N_0) is the initial amount of (^{14}C) in the living organism,
- (N(t)) is the measured amount of (^{14}C) in the sample,
- (\lambda) is the decay constant of (^{14}C).
-
Calibration: The radiocarbon age is often calibrated to account for variations in the atmospheric (^{14}C) concentration over time. These variations are due to changes in cosmic ray flux and the carbon cycle. Calibration curves, derived from dating samples of known age (such as tree rings), are used to convert the radiocarbon age into a calendar age.
Applications of Carbon-14 Dating
Radiocarbon dating has revolutionized many fields of study, providing a powerful tool for determining the age of organic materials. Some key applications include:
- Archaeology:
- Dating ancient artifacts and human remains to understand the history and culture of past civilizations.
- Determining the age of archaeological sites and settlements.
- Studying the diet and migration patterns of ancient populations.
- Geology:
- Dating sediments and organic matter in geological formations.
- Reconstructing past environmental conditions and climate changes.
- Studying the timing of geological events, such as volcanic eruptions and earthquakes.
- Paleontology:
- Dating fossilized remains of plants and animals.
- Understanding the evolution and extinction of species.
- Reconstructing ancient ecosystems.
- Environmental Science:
- Studying the age and origin of organic pollutants in the environment.
- Tracing the movement of carbon in ecosystems.
- Assessing the impact of human activities on the carbon cycle.
- Art History:
- Authenticating and dating artworks made from organic materials.
- Studying the techniques and materials used by artists in the past.
- Understanding the provenance of historical objects.
Limitations and Considerations
While radiocarbon dating is a powerful and versatile technique, it has certain limitations and considerations that must be taken into account:
- Age Range: Radiocarbon dating is most accurate for samples that are between 500 and 50,000 years old. Beyond this range, the amount of (^{14}C) remaining in the sample is too small to be measured accurately.
- Sample Contamination: Contamination of the sample with modern carbon can lead to inaccurate dating results. Careful sample collection and pretreatment are essential to minimize the risk of contamination.
- Reservoir Effects: Samples from certain environments (such as marine or freshwater environments) may have (^{14}C/^{12}C) ratios that are different from the atmosphere. This can lead to inaccurate dating results if not properly accounted for.
- Calibration Issues: The accuracy of radiocarbon dating depends on the availability of reliable calibration curves. Variations in the atmospheric (^{14}C) concentration over time can introduce uncertainties in the dating results.
- Sample Size: The size of the sample required for radiocarbon dating depends on the method used (radiometric dating or AMS) and the age of the sample. AMS requires much smaller sample sizes than radiometric dating.
Practical Examples and Calculations
Let's go through a few practical examples to illustrate how the decay equation is used in radiocarbon dating.
Example 1: Determining the Age of a Wooden Artifact
An archaeologist discovers a wooden artifact and sends it to a lab for radiocarbon dating. The lab determines that the artifact contains 25% of the original Carbon-14 that would be found in living wood. What is the age of the artifact?
Using the decay equation:
[ N(t) = N_0 e^{-\lambda t} ]
We know that (N(t) = 0.25 N_0), and (\lambda = 1.21 \times 10^{-4} \text{ years}^{-1}). We want to find (t).
[ 0.25 N_0 = N_0 e^{-1.21 \times 10^{-4} t} ]
Divide both sides by (N_0):
[ 0.25 = e^{-1.21 \times 10^{-4} t} ]
Take the natural logarithm of both sides:
[ \ln(0.25) = -1.21 \times 10^{-4} t ]
Solve for (t):
[ t = \frac{\ln(0.25)}{-1.21 \times 10^{-4}} ]
[ t \approx \frac{-1.386}{-1.21 \times 10^{-4}} \approx 11,455 \text{ years} ]
Therefore, the artifact is approximately 11,455 years old.
Example 2: Calculating the Remaining Carbon-14 in a Sample
A sample is known to be 10,000 years old. What percentage of its original Carbon-14 remains?
Using the decay equation:
[ N(t) = N_0 e^{-\lambda t} ]
We want to find the ratio (N(t)/N_0), given (t = 10,000 \text{ years}) and (\lambda = 1.21 \times 10^{-4} \text{ years}^{-1}).
[ \frac{N(t)}{N_0} = e^{-1.21 \times 10^{-4} \times 10,000} ]
[ \frac{N(t)}{N_0} = e^{-1.21} ]
[ \frac{N(t)}{N_0} \approx 0.298 ]
Therefore, approximately 29.8% of the original Carbon-14 remains in the sample.
Advanced Concepts and Corrections
In practice, radiocarbon dating involves more sophisticated corrections and considerations to improve accuracy and reliability.
-
Isotope Fractionation: Isotope fractionation refers to the slight differences in the way isotopes of an element are processed due to their mass differences. In the context of radiocarbon dating, plants discriminate slightly between (^{14}C) and (^{12}C) during photosynthesis. This leads to variations in the initial (^{14}C/^{12}C) ratio among different types of plants.
To correct for isotope fractionation, scientists measure the ratio of (^{13}C) to (^{12}C) in the sample. The (^{13}C/^{12}C) ratio is related to the degree of isotope fractionation, and this information is used to normalize the (^{14}C) measurement.
-
Atmospheric Variations: The concentration of (^{14}C) in the atmosphere has not been constant over time. Variations in cosmic ray flux, changes in the Earth's magnetic field, and the burning of fossil fuels (which releases carbon depleted in (^{14}C)) have all affected the atmospheric (^{14}C) concentration.
To account for these variations, radiocarbon dates are calibrated using calibration curves. These curves are generated by dating samples of known age, such as tree rings and sediments, using independent methods (e.g., dendrochronology and uranium-thorium dating).
-
Reservoir Effects: Samples from certain environments, such as marine or freshwater systems, may not be in equilibrium with the atmosphere. This can lead to reservoir effects, where the initial (^{14}C/^{12}C) ratio in the sample is different from that of the atmosphere.
For example, marine organisms incorporate carbon from dissolved inorganic carbon in seawater, which may be depleted in (^{14}C) due to slow mixing with the atmosphere. To correct for reservoir effects, scientists use reservoir correction factors, which are estimated based on the specific environment and the type of sample.
-
Statistical Considerations: Radiocarbon dating involves statistical measurements, and the uncertainty associated with the measurements must be taken into account. The uncertainty is typically expressed as a standard deviation ((\sigma)), and the radiocarbon age is reported as (t \pm \sigma).
When comparing radiocarbon dates, it is important to consider the uncertainties and to use statistical methods to determine whether the dates are significantly different.
Future Trends in Radiocarbon Dating
The field of radiocarbon dating continues to evolve with advances in technology and methodology. Some future trends include:
- Increased Precision and Accuracy: Ongoing improvements in AMS technology are leading to higher precision and accuracy in radiocarbon dating. This will allow scientists to date smaller samples and to resolve finer-scale chronological variations.
- Expanded Applications: Radiocarbon dating is being applied to an increasing range of research questions, including studies of climate change, environmental pollution, and human health.
- Integration with Other Dating Methods: Radiocarbon dating is often used in conjunction with other dating methods, such as luminescence dating and uranium-series dating, to provide a more comprehensive and robust chronology.
- Development of New Calibration Curves: Scientists are continuously working to develop new and improved calibration curves that cover a wider range of time periods and geographic regions.
- Automation and High-Throughput Analysis: Automation and high-throughput analysis techniques are being developed to increase the efficiency and cost-effectiveness of radiocarbon dating.
The Broader Significance of the Decay Equation
The decay equation for Carbon-14 is not just a tool for dating; it's a window into understanding fundamental physical processes. The exponential decay described by the equation is a common phenomenon in nature, applicable not only to radioactive isotopes but also to various other processes such as drug metabolism, population dynamics, and capacitor discharge in electronics.
The predictability and reliability of the decay process highlight the underlying order in what might seem like random events at the atomic level. This understanding is crucial for many scientific and technological applications, from nuclear medicine to environmental monitoring.
Conclusion
The equation for the decay of Carbon-14 is a cornerstone of radiocarbon dating, providing a powerful tool for determining the age of organic materials. Understanding this equation and its applications is essential for researchers in various fields, including archaeology, geology, paleontology, and environmental science. The principles of radiocarbon dating have not only expanded our knowledge of the past but have also contributed to our understanding of fundamental physical processes and the interconnectedness of life on Earth. As technology continues to advance, radiocarbon dating will undoubtedly remain a vital tool for unraveling the mysteries of our planet's history.
Latest Posts
Latest Posts
-
Is Water A Mixture Or Pure Substance
Nov 16, 2025
-
What Is Duties Of A Citizen
Nov 16, 2025
-
Is Magnesium A Cation Or Anion
Nov 16, 2025
-
Role Of Carbon In Biological Systems
Nov 16, 2025
-
Temple Of The Sun Machu Picchu
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about Equation For Decay Of Carbon 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.