Avogadro's Number Is Equal To 6.02x1023
penangjazz
Nov 25, 2025 · 11 min read
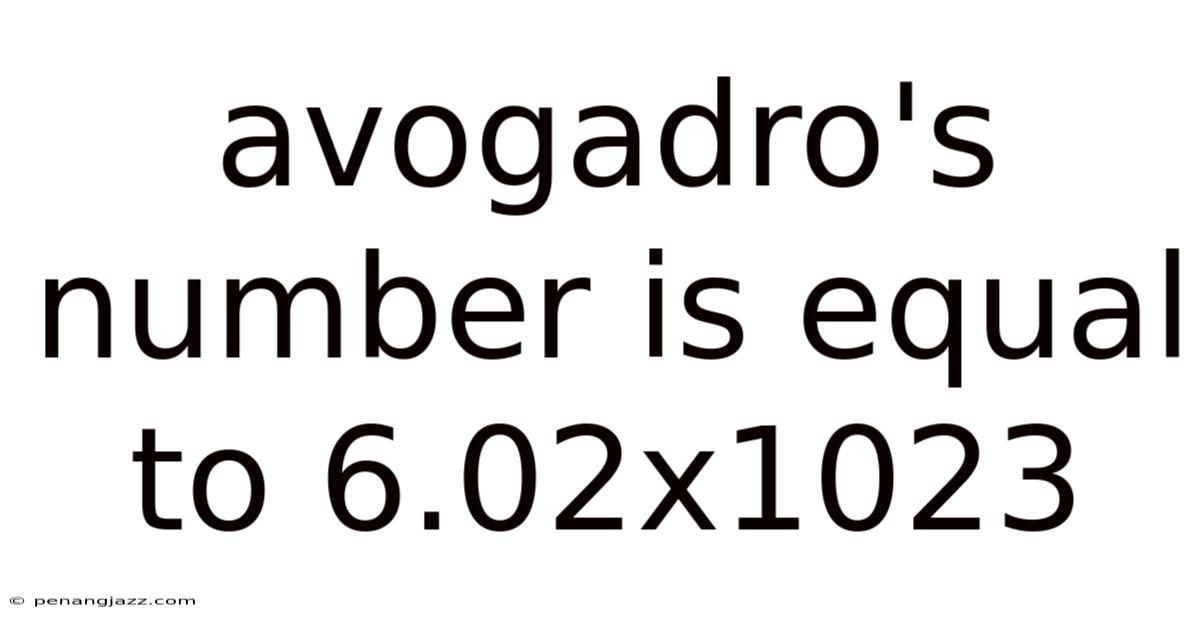
Table of Contents
The concept of Avogadro's number, a cornerstone in the field of chemistry, elegantly bridges the macroscopic world we experience and the microscopic realm of atoms and molecules. Defined as 6.02 x 10^23, this seemingly arbitrary number serves as a fundamental constant, providing a universal link between the number of entities (atoms, molecules, ions, etc.) and the amount of substance, measured in moles. Understanding Avogadro's number is crucial for quantitative analysis, stoichiometric calculations, and comprehending the very fabric of matter.
A Historical Glimpse: Unveiling the Man Behind the Number
While the number bears his name, Amedeo Avogadro himself didn't directly determine its value. Avogadro, an Italian scientist born in the late 18th century, proposed what is now known as Avogadro's Law in 1811. This law stated that equal volumes of all gases, at the same temperature and pressure, contain the same number of molecules. This groundbreaking hypothesis, though initially met with skepticism, laid the foundation for understanding the relationship between gas volume and the number of particles present.
The actual determination of Avogadro's number came later, primarily through the work of physicists like Jean Perrin in the early 20th century. Perrin's experiments on Brownian motion, the random movement of particles suspended in a fluid, provided strong evidence for the existence of atoms and allowed for the calculation of Avogadro's number. His work was so impactful that it earned him the Nobel Prize in Physics in 1926. While Perrin's method was pivotal, numerous other techniques have since been developed to refine the value of Avogadro's number, solidifying its place as a fundamental constant.
Defining the Mole: Avogadro's Number as the Bridge
At the heart of Avogadro's number lies the concept of the mole. The mole (symbol: mol) is the SI unit of amount of substance. It is defined as the amount of substance containing exactly 6.02214076 × 10^23 elementary entities. This definition officially connects the microscopic world of atoms and molecules to the macroscopic world we can measure and observe.
Think of the mole like a "chemist's dozen." A dozen always represents 12 items, whether it's a dozen eggs or a dozen donuts. Similarly, a mole always represents 6.02 x 10^23 entities, regardless of whether those entities are atoms of gold, molecules of water, or ions of sodium chloride.
The mole provides a convenient way to work with the incredibly small masses of individual atoms and molecules. Instead of dealing with impossibly small numbers like the mass of a single atom in grams, we can use molar mass, which is the mass of one mole of a substance in grams. This allows us to perform calculations and experiments with measurable quantities.
Calculating with Avogadro's Number: Practical Applications
Avogadro's number is not just a theoretical concept; it is a powerful tool used in countless calculations in chemistry and related fields. Here are some key applications:
-
Converting between moles and number of particles: This is the most fundamental application.
- To find the number of particles in a given number of moles, multiply the number of moles by Avogadro's number.
- To find the number of moles in a given number of particles, divide the number of particles by Avogadro's number.
Example: How many water molecules are there in 0.5 moles of water?
Number of molecules = 0.5 mol * 6.02 x 10^23 molecules/mol = 3.01 x 10^23 molecules
-
Relating mass to number of particles: This involves using molar mass as an intermediary.
- To find the number of particles in a given mass of a substance, first convert the mass to moles using the molar mass, then multiply by Avogadro's number.
- To find the mass of a given number of particles, first convert the number of particles to moles using Avogadro's number, then multiply by the molar mass.
Example: What is the mass of 1.204 x 10^24 atoms of carbon? (Molar mass of carbon = 12.01 g/mol)
Moles of carbon = 1.204 x 10^24 atoms / 6.02 x 10^23 atoms/mol = 2 mol Mass of carbon = 2 mol * 12.01 g/mol = 24.02 g
-
Determining empirical and molecular formulas: Avogadro's number is essential for determining the simplest whole-number ratio of atoms in a compound (empirical formula) and the actual number of atoms of each element in a molecule (molecular formula). This often involves experimental determination of elemental composition by mass and subsequent conversion to moles using molar masses and Avogadro's number.
-
Stoichiometry: Stoichiometry deals with the quantitative relationships between reactants and products in chemical reactions. Avogadro's number, through the mole concept, allows us to predict the amount of reactants needed and products formed in a given reaction.
Beyond Calculations: Conceptual Significance
Beyond its practical applications, Avogadro's number holds significant conceptual importance:
-
Evidence for the atomic theory: The very existence of Avogadro's number and the ability to experimentally determine its value provide strong evidence for the atomic theory of matter, which states that all matter is composed of discrete particles called atoms.
-
Understanding the scale of the microscopic world: Avogadro's number highlights the incredibly small size of atoms and molecules. It emphasizes that even a seemingly small amount of a substance contains an enormous number of individual particles.
-
Connecting macroscopic and microscopic properties: Avogadro's number provides a bridge between the macroscopic properties we can measure (like mass and volume) and the microscopic properties of individual atoms and molecules (like mass and size). This connection is essential for understanding the behavior of matter at all scales.
Methods for Determining Avogadro's Number: A Journey Through Scientific Ingenuity
The determination of Avogadro's number has been a testament to scientific ingenuity, involving a variety of experimental techniques across different scientific disciplines. Here are some of the key methods employed:
-
Electrolysis: Electrolysis is the process of using electricity to drive a non-spontaneous chemical reaction. One classic method involves the electrolysis of water to produce hydrogen and oxygen gas. By carefully measuring the volume of gas produced and knowing the charge passed through the electrolytic cell (related to the number of electrons transferred), Avogadro's number can be calculated. This method relies on Faraday's laws of electrolysis, which relate the amount of substance produced at an electrode to the quantity of electricity passed.
-
Brownian Motion: As mentioned earlier, Jean Perrin's work on Brownian motion was crucial in determining Avogadro's number. Brownian motion is the random movement of particles suspended in a fluid, caused by collisions with the constantly moving molecules of the fluid. By meticulously observing and analyzing the movement of these particles, Perrin was able to determine the size of the molecules and, consequently, Avogadro's number. This method elegantly connects the macroscopic observation of particle movement to the microscopic world of molecular collisions.
-
X-ray Crystallography: X-ray crystallography is a powerful technique used to determine the atomic and molecular structure of crystalline solids. By shining X-rays onto a crystal and analyzing the diffraction pattern produced, scientists can determine the arrangement of atoms within the crystal lattice and the unit cell volume. Knowing the density of the crystal and the molar mass of the substance, Avogadro's number can be calculated. This method provides a direct link between the macroscopic properties of a crystal and its microscopic structure.
-
Oil Drop Experiment: While primarily known for determining the charge of an electron, Robert Millikan's oil drop experiment also contributed to the determination of Avogadro's number. By carefully balancing the gravitational and electric forces on charged oil droplets, Millikan was able to determine the elementary charge (the charge of a single electron). Knowing the Faraday constant (the charge of one mole of electrons), Avogadro's number can be calculated by dividing the Faraday constant by the elementary charge.
-
Counting Atoms (Advanced Techniques): Modern techniques involve directly counting atoms or ions using advanced instrumentation. For example, techniques like ion trap mass spectrometry can isolate and count individual ions with high precision. While these methods are highly sophisticated, they offer the most direct route to determining Avogadro's number.
Each of these methods relies on different physical principles and experimental setups, yet they all converge on a remarkably consistent value for Avogadro's number. This convergence provides strong support for the validity of the atomic theory and the fundamental nature of Avogadro's number.
The Importance of Precision: Why the Exact Value Matters
While we often use the approximation 6.02 x 10^23, the officially accepted value of Avogadro's number is 6.02214076 × 10^23. The increased precision is not merely an academic exercise; it has significant implications for accurate scientific measurements and standards.
-
Defining the Kilogram: In 2019, the International System of Units (SI) underwent a major revision. The kilogram, previously defined by a physical artifact (the International Prototype Kilogram), was redefined in terms of fundamental constants, including the Planck constant and Avogadro's number. This redefinition ensures that the kilogram is based on unchanging physical principles, rather than a potentially unstable physical object.
-
Accurate Molar Mass Determinations: The precise value of Avogadro's number is crucial for accurate determination of molar masses. Molar mass is a fundamental property used in countless chemical calculations, and even small errors in its value can propagate through subsequent calculations.
-
Advancements in Nanotechnology: As nanotechnology advances, the ability to manipulate and characterize matter at the atomic and molecular level becomes increasingly important. The precise value of Avogadro's number is essential for accurately determining the size and number of atoms in nanoscale materials.
Common Misconceptions and Clarifications
Avogadro's number, while conceptually straightforward, can sometimes lead to misunderstandings. Here are some common misconceptions and clarifications:
-
Misconception: Avogadro's number is a physical property of a substance.
- Clarification: Avogadro's number is a number, not a physical property. It's a defined constant that relates the number of entities to the amount of substance (the mole). It doesn't change depending on the substance.
-
Misconception: One mole of any substance has the same mass.
- Clarification: One mole of any substance contains the same number of particles (6.02 x 10^23), but the mass of one mole varies depending on the substance's molar mass. For example, one mole of hydrogen has a much smaller mass than one mole of gold.
-
Misconception: Avogadro's number only applies to atoms and molecules.
- Clarification: Avogadro's number can apply to any type of entity, including ions, electrons, photons, or even hypothetical particles. The key is that it represents the number of entities in one mole.
Avogadro's Number in Everyday Life: Beyond the Chemistry Lab
While primarily a concept used in chemistry and physics, Avogadro's number and the mole concept have indirect relevance to our everyday lives.
-
Cooking and Baking: While you might not explicitly calculate moles when baking a cake, the recipes rely on precise ratios of ingredients, which ultimately relate to the number of molecules interacting. Understanding the mole concept provides a deeper appreciation for the precision required for successful cooking.
-
Pharmaceuticals: The accurate dosage of medications is critical for their effectiveness and safety. Pharmaceutical companies use the mole concept and Avogadro's number to ensure that each pill or injection contains the correct amount of active ingredient.
-
Environmental Science: Environmental scientists use the mole concept to measure and analyze pollutants in the air and water. Understanding the concentration of pollutants in terms of moles per liter or parts per million requires a grasp of Avogadro's number.
-
Material Science: The development of new materials with specific properties relies on understanding the arrangement and bonding of atoms at the microscopic level. Avogadro's number is essential for calculating the number of atoms needed to create a material with desired characteristics.
The Future of Avogadro's Number: Continued Refinement and New Applications
The story of Avogadro's number is far from over. Scientists continue to refine its value using increasingly sophisticated techniques. Furthermore, the ongoing development of new technologies will likely lead to novel applications of Avogadro's number in various fields.
-
Quantum Computing: Quantum computing, a revolutionary approach to computation, relies on manipulating individual atoms and molecules. Precise knowledge of Avogadro's number and the ability to control matter at the atomic level are crucial for building and operating quantum computers.
-
Materials Science: Advances in materials science are pushing the boundaries of what is possible with new materials. Understanding the relationship between atomic structure and macroscopic properties, mediated by Avogadro's number, is essential for designing materials with unprecedented strength, conductivity, and other desirable characteristics.
-
Cosmology: Surprisingly, Avogadro's number even finds applications in cosmology. Estimating the number of particles in the universe relies on understanding the fundamental constants, including Avogadro's number, and the composition of matter.
Conclusion: A Constant Connection to the Microscopic World
Avogadro's number, 6.02 x 10^23, is more than just a number; it is a fundamental constant that connects the macroscopic world we experience to the microscopic realm of atoms and molecules. From its historical roots in Avogadro's Law to its modern applications in defining the kilogram and advancing nanotechnology, Avogadro's number has played a crucial role in the development of science. Its significance lies not only in its practical use for calculations but also in its conceptual importance for understanding the nature of matter. As technology continues to advance, Avogadro's number will undoubtedly remain a cornerstone of scientific inquiry, bridging the gap between the observable and the infinitesimally small.
Latest Posts
Latest Posts
-
How To Find The Derivative Of Ln
Nov 25, 2025
-
The Space Between Two Neurons Is Called The
Nov 25, 2025
-
How To Find Ioc Taylor Series
Nov 25, 2025
-
Confidence Interval For Population Mean Formula
Nov 25, 2025
-
What Does A Peripheral Protein Do
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about Avogadro's Number Is Equal To 6.02x1023 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.