8 Is What Percent Of 5
penangjazz
Nov 23, 2025 · 9 min read
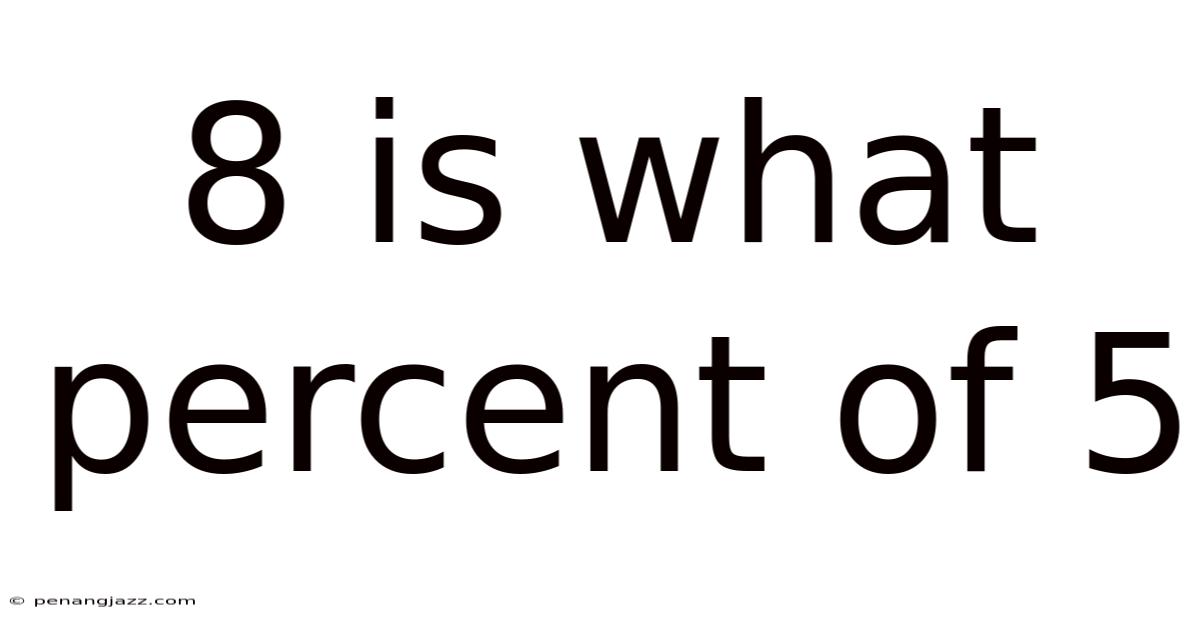
Table of Contents
Calculating percentages is a fundamental skill with applications in various aspects of life, from figuring out discounts while shopping to understanding financial data. When faced with the question "8 is what percent of 5?", understanding the underlying concepts and steps involved is crucial. This article will thoroughly explain how to solve this type of percentage problem, providing a clear and detailed methodology that anyone can follow. Whether you're a student, a professional, or simply someone looking to brush up on your math skills, this guide will provide the necessary tools and insights to master percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." Essentially, a percentage tells you how much of a whole something represents. For example, if you score 80% on a test, it means you got 80 out of every 100 possible points.
Percentages are widely used because they provide a standardized way to compare different quantities. Instead of comparing raw numbers, which can be confusing when the totals are different, percentages allow for easy comparison by scaling everything to a common base of 100.
In the context of the question "8 is what percent of 5?", we are trying to determine what proportion 8 represents when compared to 5, expressed as a percentage. This means we want to find out what number, when divided by 100, gives us the ratio of 8 to 5.
The Formula for Calculating Percentages
To calculate what percent one number is of another, you can use a simple formula:
Percentage = (Part / Whole) * 100
Where:
- Part is the number you are comparing (in this case, 8).
- Whole is the number you are comparing against (in this case, 5).
This formula works because it first calculates the fraction that the "part" represents of the "whole," and then multiplies that fraction by 100 to convert it into a percentage.
Applying the Formula to "8 is what percent of 5?"
Using the formula, we can plug in the numbers:
Percentage = (8 / 5) * 100
Let's break down the calculation step-by-step:
-
Divide the Part by the Whole:
8 / 5 = 1.6 -
Multiply by 100 to Convert to Percentage:
1. 6 * 100 = 160
Therefore, 8 is 160% of 5. This means that 8 is significantly larger than 5, specifically 1.6 times larger.
Step-by-Step Guide to Solving the Problem
To ensure clarity, let's go through a detailed step-by-step guide on how to solve the problem "8 is what percent of 5?".
Step 1: Identify the Part and the Whole
The first step is to correctly identify which number is the "part" and which is the "whole." In this case:
- Part: 8
- Whole: 5
It’s essential to understand that the "whole" is the base or the reference number against which the "part" is being compared.
Step 2: Set Up the Fraction
Once you have identified the part and the whole, set up the fraction:
Fraction = Part / Whole = 8 / 5
This fraction represents the ratio of 8 to 5.
Step 3: Perform the Division
Divide the part (8) by the whole (5):
8 ÷ 5 = 1.6
This gives you the decimal equivalent of the fraction.
Step 4: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100:
1. 6 * 100 = 160
This gives you the percentage.
Step 5: State the Answer
Finally, state the answer clearly:
8 is 160% of 5.
This means that 8 is 160 percent of 5, which indicates that 8 is larger than 5.
Understanding When the Percentage is Greater Than 100%
In the example "8 is what percent of 5?", the percentage is greater than 100%. This can be confusing, but it simply means that the "part" is larger than the "whole." When the part is larger than the whole, the percentage will always be greater than 100%.
For example:
- If you have 15 apples and you want to know what percent 15 is of 10, the answer is 150%.
- If a company's revenue increases from $100,000 to $150,000, the increase is 150% of the original revenue when considering the new revenue relative to a base of 100.
Common Mistakes to Avoid
When calculating percentages, it’s important to avoid common mistakes that can lead to incorrect answers:
-
Incorrectly Identifying the Part and the Whole:
- This is the most common mistake. Always ensure you know which number is being compared (the part) and which number is the base (the whole).
-
Forgetting to Multiply by 100:
- After dividing the part by the whole, you must multiply the result by 100 to convert it into a percentage. Failing to do so will leave you with a decimal or fraction, not a percentage.
-
Misinterpreting the Question:
- Sometimes the wording of the question can be confusing. Read the question carefully to understand what exactly is being asked.
-
Rounding Errors:
- If the division results in a long decimal, rounding too early can lead to inaccuracies. It's best to round only at the final step.
-
Using the Wrong Formula:
- Ensure you are using the correct formula for the type of percentage problem you are solving. The formula (Part / Whole) * 100 is specifically for finding what percentage one number is of another.
Real-World Applications
Understanding how to calculate percentages is useful in many real-world situations. Here are a few examples:
-
Finance:
- Calculating investment returns: If you invest $1,000 and it grows to $1,200, the return is 20% (($200 / $1,000) * 100).
- Determining interest rates: If you borrow $5,000 and pay $5,500 back, the interest is 10% (($500 / $5,000) * 100).
-
Retail:
- Calculating discounts: If an item is 25% off and originally costs $80, the discount is $20 (0.25 * $80).
- Understanding sales tax: If an item costs $100 and the sales tax is 6%, the tax amount is $6 (0.06 * $100).
-
Education:
- Calculating grades: If you score 75 out of 100 on a test, your grade is 75%.
- Tracking progress: If you have completed 60% of a course, you know you have 40% left to finish.
-
Health:
- Monitoring weight loss: If you lose 10 pounds from an original weight of 200 pounds, you've lost 5% of your weight ((10 / 200) * 100).
- Understanding medication dosages: If a medication is 5% solution, it means there are 5 parts of the active ingredient per 100 parts of the solution.
-
Business:
- Analyzing market share: If a company has 30% of the market, it means they control 30 out of every 100 units sold.
- Tracking sales growth: If sales increase from $500,000 to $600,000, the growth is 20% (($100,000 / $500,000) * 100).
Advanced Percentage Problems
Once you've mastered the basics, you can tackle more complex percentage problems. Here are a few examples:
Example 1: Finding the Original Price After a Discount
A shirt is sold for $30 after a 25% discount. What was the original price?
-
Understand the Problem:
- The sale price ($30) is 75% of the original price (100% - 25% discount).
-
Set Up the Equation:
-
- 75 * Original Price = $30
-
-
Solve for the Original Price:
- Original Price = $30 / 0.75 = $40
So, the original price of the shirt was $40.
Example 2: Calculating Percentage Increase
A company's revenue increased from $200,000 to $250,000. What is the percentage increase?
-
Calculate the Amount of Increase:
- Increase = $250,000 - $200,000 = $50,000
-
Divide the Increase by the Original Amount:
- $50,000 / $200,000 = 0.25
-
Multiply by 100 to Convert to Percentage:
-
- 25 * 100 = 25%
-
So, the company's revenue increased by 25%.
Example 3: Calculating Compound Percentage Changes
A stock increases by 10% in the first year and then decreases by 5% in the second year. What is the overall percentage change?
-
Start with an Initial Value:
- Assume the initial value of the stock is $100.
-
Calculate the Value After the First Year:
- Increase of 10%: $100 + (0.10 * $100) = $110
-
Calculate the Value After the Second Year:
- Decrease of 5%: $110 - (0.05 * $110) = $104.50
-
Calculate the Overall Change:
- Overall Change = $104.50 - $100 = $4.50
-
Calculate the Percentage Change:
- Percentage Change = ($4.50 / $100) * 100 = 4.5%
So, the stock's overall percentage change is an increase of 4.5%.
Tips for Improving Your Percentage Calculation Skills
-
Practice Regularly:
- The more you practice, the more comfortable you will become with percentage calculations. Use online resources, textbooks, and real-life examples to practice.
-
Understand the Concepts:
- Don't just memorize formulas. Understand the underlying concepts of percentages and how they relate to fractions and decimals.
-
Use Real-World Examples:
- Apply percentage calculations to everyday situations, such as calculating discounts while shopping or figuring out tips at restaurants.
-
Check Your Answers:
- Whenever possible, check your answers to ensure they make sense. If you're calculating a discount, make sure the final price is lower than the original price.
-
Use Technology:
- Use calculators and spreadsheet software to help with complex calculations. However, make sure you understand the process and can do the calculations manually as well.
-
Break Down Problems:
- Break down complex problems into smaller, more manageable steps. This will make the problem less daunting and easier to solve.
Conclusion
Calculating percentages is a critical skill with numerous practical applications. Whether you're determining discounts, analyzing financial data, or understanding statistical information, the ability to work with percentages is essential. By understanding the basic formula (Part / Whole) * 100 and practicing regularly, you can master percentage calculations and apply them confidently in various aspects of your life.
In the specific case of "8 is what percent of 5?", the answer is 160%. This demonstrates that 8 is larger than 5 and represents 160% of its value. By following the step-by-step guide and avoiding common mistakes, you can accurately solve similar percentage problems and enhance your mathematical proficiency. Remember to identify the part and the whole correctly, perform the division, and multiply by 100 to convert the result into a percentage. With consistent practice and a solid understanding of the concepts, you can become proficient in percentage calculations and use this skill effectively in your personal and professional life.
Latest Posts
Latest Posts
-
Hexagonal Close Packed Atoms Per Unit Cell
Nov 23, 2025
-
Laser Light Amplification By Stimulated Emission Of Radiation
Nov 23, 2025
-
What Is The Leading Term In A Polynomial
Nov 23, 2025
-
What Are The Freezing And Boiling Points Of Water
Nov 23, 2025
-
How To Calculate Change In Gibbs Free Energy
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.