1 2 Addition 1 4 Addition
penangjazz
Nov 18, 2025 · 10 min read
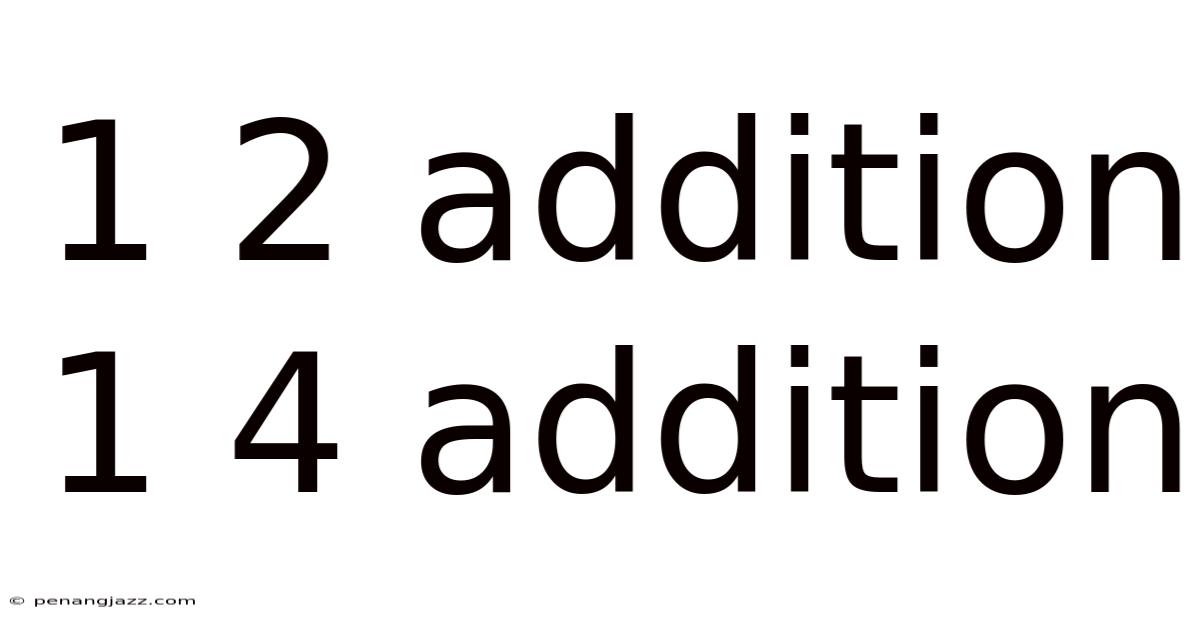
Table of Contents
Let's embark on a journey into the realm of fractions, specifically focusing on the addition of 1/2 and 1/4. While seemingly simple, this operation unveils fundamental principles of fraction manipulation and provides a solid foundation for more complex arithmetic. Mastering this concept not only enhances your mathematical toolkit but also sharpens your problem-solving skills applicable in various real-world scenarios. Understanding 1/2 + 1/4 is a stepping stone to conquering more intricate fractional calculations.
Unveiling the Basics: Fractions Demystified
Before diving into the addition itself, let's establish a clear understanding of what fractions represent. A fraction, in its essence, represents a part of a whole. It's composed of two primary components:
- Numerator: The number above the fraction bar, indicating the number of parts you possess.
- Denominator: The number below the fraction bar, denoting the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, '1' is the numerator, signifying one part, and '2' is the denominator, representing that the whole is divided into two equal parts. Similarly, in 1/4, '1' is the numerator, and '4' is the denominator. Visualizing fractions is crucial. Imagine a pizza cut into two equal slices. One slice represents 1/2 of the pizza. Now, picture the same pizza cut into four equal slices. One slice now represents 1/4 of the pizza.
The Challenge of Adding Unlike Fractions
The core challenge when adding fractions like 1/2 and 1/4 lies in the fact that they have different denominators. We can only directly add fractions that share a common denominator. Think of it like trying to add apples and oranges – they are different units. To add them meaningfully, you need a common unit, such as "fruits." Similarly, fractions need a common denominator to be added directly. The denominator dictates the size of the "slices" we are dealing with. So, how do we achieve this common ground? This is where the concept of the Least Common Multiple (LCM) comes into play.
Finding the Common Ground: Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two numbers is the smallest number that is a multiple of both. In the context of fraction addition, the LCM of the denominators becomes our common denominator. Let's find the LCM of 2 (the denominator of 1/2) and 4 (the denominator of 1/4).
- Multiples of 2: 2, 4, 6, 8, 10…
- Multiples of 4: 4, 8, 12, 16, 20…
As you can see, the smallest number that appears in both lists is 4. Therefore, the LCM of 2 and 4 is 4. This means we need to convert both fractions to have a denominator of 4.
Transforming Fractions: Equivalent Fractions
Now that we've identified the common denominator (4), we need to convert 1/2 into an equivalent fraction with a denominator of 4. An equivalent fraction represents the same value as the original fraction but with a different numerator and denominator. To achieve this, we multiply both the numerator and the denominator of 1/2 by the same number. In this case, we need to multiply the denominator (2) by 2 to get 4. Therefore, we also multiply the numerator (1) by 2.
1/2 * (2/2) = 2/4
Notice that we are essentially multiplying by 1 (2/2 = 1), which doesn't change the value of the fraction, only its representation. The fraction 2/4 is equivalent to 1/2. It simply represents the same amount divided into more, but smaller, parts. The fraction 1/4 already has the desired denominator, so we don't need to modify it. It remains as 1/4.
The Moment of Truth: Adding Fractions with Common Denominators
With both fractions now sharing a common denominator, the addition becomes straightforward. We simply add the numerators while keeping the denominator the same.
2/4 + 1/4 = (2 + 1)/4 = 3/4
Therefore, 1/2 + 1/4 = 3/4.
Visualizing the Solution: A Pie Chart Perspective
Imagine a pie cut into four equal slices. The fraction 1/4 represents one of those slices. Now, consider that 1/2 of the pie is equivalent to two of those slices (2/4). Adding 1/4 to 1/2 (or 2/4) means adding one more slice to the two already present. This results in three slices out of the four, which is represented by the fraction 3/4.
A Step-by-Step Guide: Mastering the Addition Process
Let's formalize the process into a clear, step-by-step guide for adding 1/2 and 1/4:
- Identify the Fractions: Recognize the fractions you need to add (1/2 and 1/4).
- Find the LCM: Determine the Least Common Multiple of the denominators (2 and 4). The LCM is 4.
- Create Equivalent Fractions: Convert each fraction into an equivalent fraction with the LCM as the denominator.
- 1/2 becomes 2/4 (multiply numerator and denominator by 2).
- 1/4 remains 1/4 (already has the desired denominator).
- Add the Numerators: Add the numerators of the equivalent fractions while keeping the denominator the same.
- 2/4 + 1/4 = (2+1)/4 = 3/4
- Simplify (If Possible): Check if the resulting fraction can be simplified. In this case, 3/4 is already in its simplest form.
Beyond the Basics: Real-World Applications
The ability to add fractions is not just an abstract mathematical skill; it has practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often involve fractional measurements. For example, you might need 1/2 cup of flour and 1/4 cup of sugar. Adding these fractions allows you to accurately measure the ingredients.
- Construction and Carpentry: When working with wood or other materials, you might need to add fractional lengths. For instance, you might need a piece of wood that is 1/2 foot long and another piece that is 1/4 foot long.
- Time Management: Dividing tasks into smaller segments can be represented with fractions. If you spend 1/2 hour on one task and 1/4 hour on another, you can calculate the total time spent.
- Financial Planning: Budgeting often involves dividing income into different categories represented by fractions. You might allocate 1/2 of your income to expenses and 1/4 to savings.
Common Mistakes and How to Avoid Them
While the addition of 1/2 and 1/4 is relatively straightforward, some common mistakes can occur. Being aware of these pitfalls can help you avoid them:
- Adding Numerators and Denominators Directly: A frequent error is simply adding the numerators and denominators without finding a common denominator (e.g., 1/2 + 1/4 = 2/6). This is incorrect. You must have a common denominator before adding.
- Incorrectly Calculating the LCM: An inaccurate LCM will lead to incorrect equivalent fractions and ultimately, the wrong answer. Double-check your LCM calculation.
- Forgetting to Multiply the Numerator: When creating equivalent fractions, remember to multiply both the numerator and the denominator by the same number. Multiplying only the denominator will change the value of the fraction.
- Not Simplifying the Final Answer: Although 3/4 is already in its simplest form, some fraction additions result in fractions that can be simplified. Always check if your final answer can be reduced to its simplest form.
Exploring Different Approaches: Alternative Methods
While the LCM method is the most common and generally applicable, there are alternative approaches you can use to add 1/2 and 1/4, especially when dealing with these specific fractions:
- Visual Decomposition: Visualize 1/2 as two 1/4s. Therefore, 1/2 + 1/4 can be seen as two 1/4s plus one 1/4, resulting in three 1/4s or 3/4.
- Decimal Conversion: Convert the fractions to decimals: 1/2 = 0.5 and 1/4 = 0.25. Then add the decimals: 0.5 + 0.25 = 0.75. Convert 0.75 back to a fraction, which is 3/4. (This method is generally discouraged when learning fractions, as it bypasses the understanding of fractional operations).
Deep Dive: Why Does Finding a Common Denominator Work?
The concept of finding a common denominator might seem like a mathematical trick, but it's rooted in the fundamental principles of addition. When we add quantities, they need to be expressed in the same units. In the case of fractions, the denominator defines the "unit size." By finding a common denominator, we are essentially expressing both fractions in terms of the same-sized parts of the whole.
Imagine you have a measuring cup divided into halves and another divided into fourths. You can't directly add the amounts because the divisions are different. However, if you relabel the cup divided into halves so that it is also divided into fourths, then you can easily add the quantities because they are now measured in the same "units" (fourths of a cup). This relabeling is precisely what we are doing when we find a common denominator and create equivalent fractions.
The Psychological Aspect: Building Confidence in Math
Often, the biggest hurdle in learning mathematics is not the complexity of the concepts themselves but the fear and anxiety associated with them. Fractions, in particular, can be a source of apprehension for many. Breaking down complex problems into smaller, manageable steps can significantly boost confidence. Mastering the addition of simple fractions like 1/2 and 1/4 serves as a building block for more advanced concepts. As you successfully solve these problems, your confidence grows, making you more willing to tackle more challenging mathematical tasks.
Remember, mathematics is not about memorizing formulas but about understanding the underlying principles. When you truly understand why a particular method works, you are less likely to make mistakes and more likely to retain the information. So, focus on understanding the concepts, practice regularly, and don't be afraid to ask questions.
FAQ: Addressing Common Queries About Fraction Addition
- Q: Can I add fractions if they don't have a common denominator?
- A: No, you must find a common denominator before adding fractions.
- Q: Is the LCM always the best common denominator to use?
- A: Yes, using the LCM simplifies the process and often results in a fraction that is already in its simplest form. However, any common multiple of the denominators will work, but it may require simplification at the end.
- Q: What if I can't find the LCM easily?
- A: You can always multiply the denominators together to find a common denominator, although it might not be the least common denominator. You'll then need to simplify the resulting fraction.
- Q: Can I use a calculator to add fractions?
- A: Yes, calculators can be helpful, but it's essential to understand the underlying principles of fraction addition. Relying solely on a calculator can hinder your understanding and problem-solving skills.
- Q: What do I do if the answer is an improper fraction (numerator is greater than the denominator)?
- A: Convert the improper fraction to a mixed number (a whole number and a fraction).
Conclusion: The Power of Fractional Understanding
The addition of 1/2 and 1/4, while seemingly simple, embodies the core principles of fraction manipulation. By understanding the concepts of numerators, denominators, equivalent fractions, and the Least Common Multiple, you unlock a powerful tool for solving a wide range of mathematical problems. Moreover, mastering these foundational skills builds confidence and paves the way for more advanced mathematical learning. Remember, the key to success lies in understanding the underlying principles, practicing regularly, and approaching mathematics with a positive mindset. Embrace the challenge, and you'll discover the beauty and power of fractional understanding. From recipes to construction projects, the ability to confidently add fractions empowers you to navigate the world with greater precision and understanding.
Latest Posts
Latest Posts
-
Is Texture A Physical Or Chemical Property
Nov 18, 2025
-
Derivatives Of Exponential And Logarithmic Functions
Nov 18, 2025
-
How To Find A Height Of A Parallelogram
Nov 18, 2025
-
Magnifying Glass How Does It Work
Nov 18, 2025
-
Finding The Sum Of A Series
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Addition 1 4 Addition . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.